题目内容
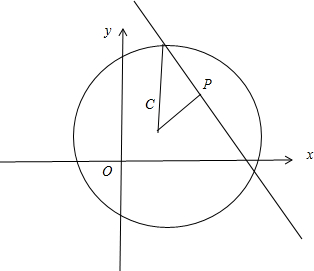
经过点(3,1)被圆C:x2+y2-2x-4y-20=0截得的弦最短的直线的方程是( )
分析:根据圆的性质可得d2=r2-(
)2(l为直线被圆截得的弦长),若使经过点(3,1)被圆C:x2+y2-2x-4y-20=0截得的弦最短,则只要圆心C到直线的距离d最大,而d≤PC,当直线l与PC垂直时,dmax=PC,从而可求直线方程
| l |
| 2 |
解答:解:由题意可得圆心为C(1,2),半径r=5
根据圆的性质可得d2=r2-(
)2(l为直线被圆截得的弦长)
若使经过点(3,1)被圆C:x2+y2-2x-4y-20=0截得的弦最短,则只要圆心C到直线的距离d最大
根据题意可得,d≤PC,当直线l与PC垂直时,dmax=PC=
=
此时所求直线的斜率为k=-
=2
∴所求的直线的方程为y-1=2(x-3)整理可得2x-y-5=0
故选D
根据圆的性质可得d2=r2-(
| l |
| 2 |
若使经过点(3,1)被圆C:x2+y2-2x-4y-20=0截得的弦最短,则只要圆心C到直线的距离d最大
根据题意可得,d≤PC,当直线l与PC垂直时,dmax=PC=
| (3-1)2+(2-1)2 |
| 5 |
此时所求直线的斜率为k=-
| 1 |
| kPC |
∴所求的直线的方程为y-1=2(x-3)整理可得2x-y-5=0
故选D

点评:本题主要考查了直线与圆的相交位置关系的应用,解题的关键 是灵活利用圆性质d2=r2-(
)2(l为直线被圆截得的弦长),把所求弦的最小转化为圆心到直线的距离的最大值
| l |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目