题目内容
如果对于函数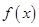 定义域内任意的
定义域内任意的 ,都有
,都有 (
( 为常数),称
为常数),称 为
为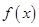 的下界,下界
的下界,下界 中的最大值叫做
中的最大值叫做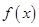 的下确界.下列函数中,有下确界的函数是( ).).
的下确界.下列函数中,有下确界的函数是( ).).
① ②
② ③
③ ④
④
| A.①② | B.①③ | C.②③④ | D.①③④ |
D
解析试题分析:解:对 ≥-1 在R上恒成立,所以此函数有下确界;
≥-1 在R上恒成立,所以此函数有下确界;
对 ∈R在(0,+∞)上恒成立,所以此函数无下确界;
∈R在(0,+∞)上恒成立,所以此函数无下确界;
对 ∈(0,+∞)在R上恒成立,所以此函数有下确界;
∈(0,+∞)在R上恒成立,所以此函数有下确界;
对 ∈{-1,0,1}在(0,+∞)上恒成立,所以此函数有下确界;
∈{-1,0,1}在(0,+∞)上恒成立,所以此函数有下确界;
综上可知①③④对应的函数都有下确界.故选D.
考点:函数的最值
点评:本题考查的是函数的最值和新定义相联系的综合类问题.在解答的过程当中充分体现了新定义问题的特点、问题转化的思想以及函数求最值的方法.值得同学们体会反思

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知 且有
且有 ,则
,则 ( )
( )
A. | B.1 | C. | D.0 |
已知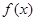 是以
是以 为周期的偶函数,且
为周期的偶函数,且 时,
时, ,则当
,则当 时,
时,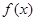 等于 ( )
等于 ( )
A. | B. | C. | D. |
终边在一、三象限角平分线的角的集合是 ( )
A. | B. |
C. | D. |
已知函数
 的部分图象如图所示,则函数
的部分图象如图所示,则函数 的解析式为( )
的解析式为( )
A. |
B. |
C. |
D. |
在 内,使
内,使 成立的
成立的 的取值范围是 ( )
的取值范围是 ( )
A. | B.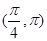 |
C. | D.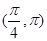  |
 的值( )
的值( )
A.小于 | B.大于 | C.等于 | D.不存在 |
设函数 ,则下列结论正确的是
,则下列结论正确的是
A.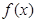 的图像关于直线 的图像关于直线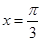 对称 对称 |
B.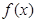 的图像关于点 的图像关于点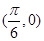 对称 对称 |
C.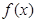 的最小正周期为 的最小正周期为 ,且在 ,且在 上为增函数 上为增函数 |
D.把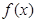 的图像向右平移 的图像向右平移 个单位,得到一个偶函数的图像 个单位,得到一个偶函数的图像 |
已知 ,且
,且 ,则
,则 ( )
( )
A.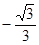 | B. | C.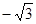 | D. |