题目内容
7.已知等比数列{an},满足a1+a2+a3+a4+a5=2,$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+\frac{1}{{a}_{3}}+\frac{1}{{a}_{4}}+\frac{1}{{a}_{5}}$=$\frac{1}{2}$,则a3=( )| A. | -2 | B. | 2 | C. | ±2 | D. | ±4 |
分析 利用等比数列的性质可得:a1a5=a2a4=${a}_{3}^{2}$,分别通分即可得出.
解答 解:∵等比数列{an},满足a1+a2+a3+a4+a5=2,$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+\frac{1}{{a}_{3}}+\frac{1}{{a}_{4}}+\frac{1}{{a}_{5}}$=$\frac{1}{2}$,
∴$\frac{{a}_{1}+{a}_{5}}{{a}_{1}{a}_{5}}$+$\frac{{a}_{2}+{a}_{4}}{{a}_{2}{a}_{4}}$+$\frac{1}{{a}_{3}}$=$\frac{1}{2}$,
∴$\frac{{a}_{1}+{a}_{5}}{{a}_{3}^{2}}$+$\frac{{a}_{2}+{a}_{4}}{{a}_{3}^{2}}$+$\frac{{a}_{3}}{{a}_{3}^{2}}$=$\frac{1}{2}$,
∴2=$\frac{1}{2}{a}_{3}^{2}$,
解得a3=±2.
故选:C.
点评 本题考查了等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0)(x1≠x2),都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$.则下列结论正确的是( )
| A. | $f({log_2}^{\frac{1}{4}})>f({0.2^3})>f(\sqrt{3})$ | B. | $f({log_2}^{\frac{1}{4}})>f(\sqrt{3})>f({0.2^3})$ | ||
| C. | $f(\sqrt{3})>f({0.2^3})>f({log_2}^{\frac{1}{4}})$ | D. | $f({0.2^3})>f(\sqrt{3})>f({log_2}^{\frac{1}{4}})$ |
15.已知下列四组散点图对应的样本统计数据的相关系数分别为r1,r2,r3,r4,则它们的大小关系为( )
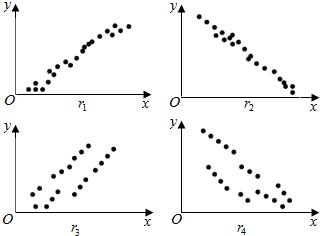

| A. | r1<r3<r4<r2 | B. | r2<r4<r3<r1 | C. | r4<r2<r1<r3 | D. | r3<r1<r2<r4 |
2.已知扇形的周长为8cm,则该扇形的面积S值最大时圆心角的大小为( )
| A. | 4弧度 | B. | 3弧度 | C. | 2弧度 | D. | 1弧度 |