题目内容
设 ,则“
,则“ ”是“直线
”是“直线 与直线
与直线 平行”的
平行”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
C
解析试题分析:利用充分、必要条件进行推导,结合两直线直线l1:A1x+B1y+C1=0与直线l2:A2x+B2y+C2=0平行的充要条件是A1B2=A2B1≠A2C1可得答案.
(1)充分性:
当a=1时,直线l1:x+2y-1=0与直线l2:x+2y+4=0平行;
(2)必要性:
当直线l1:ax+2y-1=0与直线l2:x+2y+4=0平行时有:
a•2=2•1,即:a=1.
∴“a=1”是“直线l1:ax+2y-1=0与直线l2:x+2y+4=0平行”充分必要条件.
故选C
考点:本试题主要考查了充分条件、必要条件、充分必要条件以及两直线平行的充要条件,属于基础题型,要做到熟练掌握。
点评:解决该试题的关键是对于两条直线平行的要分为斜率存在和斜率不存在两种情况来分析。两直线平行的充要条件是A1B2=A2B1≠A2C1。

练习册系列答案
相关题目
“ ”是“
”是“ ”的( )
”的( )
| A.充要条件 | B.必要而不充分条件 |
| C.充分而不必要条件 | D.既不充分也不必要 |
“ ”是“函数
”是“函数 在其定义域上为奇函数”的( )
在其定义域上为奇函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若命题“ 或
或 ”为真,“非p”为真,则( )
”为真,“非p”为真,则( )
| A.p真q真 | B.p假q真 | C.p真q假 | D.p假q假 |
已知命题 ,则非
,则非 为( )
为( )
A.? | B.?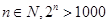 |
C.? | D.? |
已知命题 :
: ,
, ,那么下列结论正确的是( )
,那么下列结论正确的是( )
A. , , | B.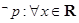 , , |
C. , , | D.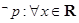 , , |
设命题甲为: ,命题乙为
,命题乙为 ,则甲是乙的( )
,则甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
下列命题中,真命题是( )
A.若 则 则 |
B.若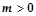 则 则 有实根 有实根 |
C.存在实数 当 当 时 时 |
D. 是 是 或 或 的充分不必要条件 的充分不必要条件 |
 :若
:若 ,则
,则 是
是 的充分而不必要条件;
的充分而不必要条件; :函数
:函数 的定义域是
的定义域是 ,则( )
,则( ) 、“
、“ 、“
、“ 、“
、“ 、“
、“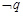 ”为真
”为真