题目内容
已知幂函数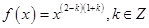 ,且
,且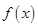 在
在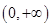 上单调递增.
上单调递增.
(1)求实数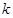 的值,并写出相应的函数
的值,并写出相应的函数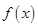 的解析式;
的解析式;
(2)若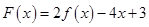 在区间
在区间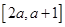 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(3)试判断是否存在正数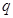 ,使函数
,使函数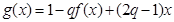 在区间
在区间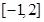 上的值域为
上的值域为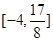 若存在,求出
若存在,求出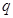 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) 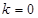 或
或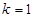 ,
,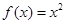 (2)
(2) 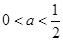 (3)
(3) 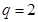
解析试题分析:(1)由题意知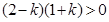 ,解得:
,解得: . 2分
. 2分
又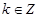 ∴
∴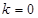 或
或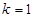 , 3分
, 3分
分别代入原函数,得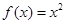 . 4分
. 4分
(2)由已知得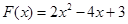 . 5分
. 5分
要使函数不单调,则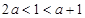 ,则
,则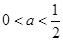 . 8分
. 8分
(3)由已知,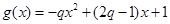 . 9分
. 9分
法一:假设存在这样的正数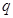 符合题意,
符合题意,
则函数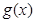 的图象是开口向下的抛物线,其对称轴为
的图象是开口向下的抛物线,其对称轴为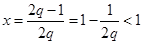 ,
,
因而,函数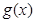 在
在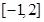 上的最小值只能在
上的最小值只能在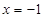 或
或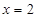 处取得,
处取得,
又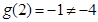 ,
,
从而必有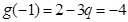 ,解得
,解得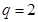 .
.
此时,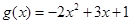 ,其对称轴
,其对称轴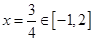 ,
,
∴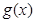 在
在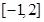 上的最大值为
上的最大值为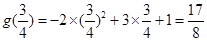 ,符合题意.
,符合题意.
∴存在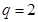 ,使函数
,使函数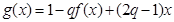 在区间
在区间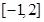 上的值域为
上的值域为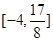 14分法二:假设存在这样的正数
14分法二:假设存在这样的正数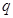 符合题意,
符合题意,
由(1)知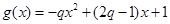 ,
,
则函数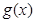 的图象是开口向下的抛物线,其对称轴为
的图象是开口向下的抛物线,其对称轴为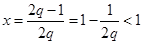 ,
,
考点:幂函数及二次函数单调性最值
点评:第二问中二次函数不单调需满足对称轴在给定区间内,第三问关于最值的考查需注意对称轴与给定区间的关系,从而确定给定区间上的单调性得到最值,一般求解时都要分情况讨论

练习册系列答案
相关题目
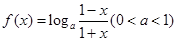 .
. 的定义域
的定义域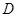 ,并判断
,并判断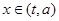 时,函数
时,函数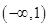 ,求
,求 与
与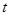 的值.
的值.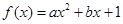 (
(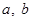 为实数,
为实数,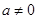 ,
,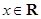 ),
),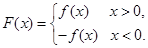
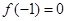 ,且函数
,且函数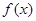 的值域为
的值域为 ,求
,求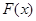 的表达式;
的表达式;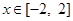 时,
时, 是单调函数,求实数
是单调函数,求实数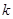 的取值范围;
的取值范围;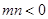 ,
,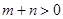 ,
,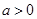 ,且函数
,且函数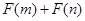 是否大于
是否大于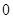 ?
?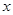 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米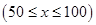 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油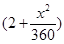 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.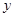 关于
关于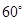 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为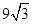 平方米,且高度不低于
平方米,且高度不低于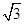 米,设防洪堤横断面的腰长为
米,设防洪堤横断面的腰长为 米,外周长(梯形的上底线段BC与两腰长的和)为
米,外周长(梯形的上底线段BC与两腰长的和)为 米.
米.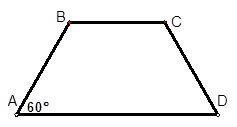
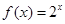 ,
,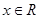 .
.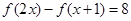 ;
;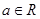 ,求函数
,求函数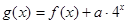 在区间
在区间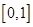 上的最大值
上的最大值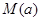 的表达式;
的表达式;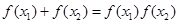 ,
,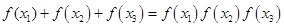 ,求
,求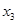 的最大值.
的最大值.