题目内容
已知函数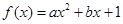 (
(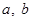 为实数,
为实数,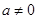 ,
,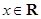 ),
),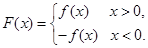
(Ⅰ)若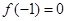 ,且函数
,且函数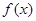 的值域为
的值域为 ,求
,求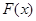 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当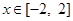 时,
时, 是单调函数,求实数
是单调函数,求实数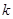 的取值范围;
的取值范围;
(Ⅲ)设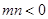 ,
,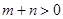 ,
,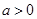 ,且函数
,且函数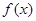 为偶函数,判断
为偶函数,判断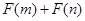 是否大于
是否大于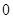 ?
?
(Ⅰ)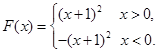 (Ⅱ)
(Ⅱ)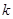 的范围是
的范围是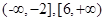 时,
时,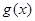 是单调函数.
是单调函数.
(Ⅲ)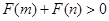 .
.
解析试题分析:(Ⅰ)因为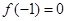 ,所以
,所以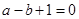 .因为
.因为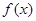 的值域为
的值域为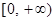 ,所以
,所以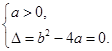 2分
2分
所以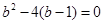 . 解得
. 解得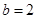 ,
,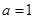 . 所以
. 所以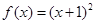 .
.
所以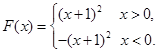 4分
4分
(Ⅱ)因为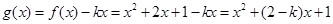
=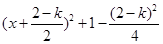 , 6分
, 6分
所以,当 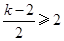 或
或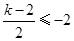 时
时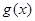 单调.
单调.
即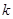 的范围是
的范围是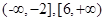 时,
时,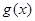 是单调函数. 8分
是单调函数. 8分
(Ⅲ)因为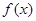 为偶函数,所以
为偶函数,所以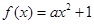 . 所以
. 所以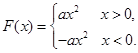 10分
10分
因为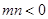 , 依条件设
, 依条件设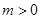 ,则
,则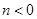 .又
.又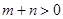 ,所以
,所以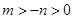 .
.
所以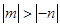 . 12分
. 12分
此时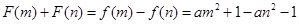
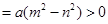 .
.
即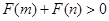 . 13分
. 13分
考点:待定系数法,二次函数的图象和性质,分段函数的概念,函数的奇偶性、单调性。
点评:中档题,利用待定系数法,确定函数的解析式,是常见考试题目。研究二次函数的图象和性质,要关注“开口方向,对称轴位置,与坐标轴交点”等。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 千件,需另投入成本为
千件,需另投入成本为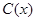 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完. (万元)关于年产量
(万元)关于年产量 人,(
人,( ,且
,且 为偶数),每人每年可创利
为偶数),每人每年可创利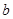 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人? 与
与 ,如果对任意
,如果对任意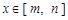 ,均有
,均有 与
与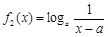 (a > 0且
(a > 0且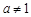 ),给定区间
),给定区间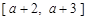 .
.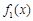 与
与 在给定区间
在给定区间 ;
; 且
且 ,求
,求 的值.
的值.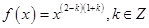 ,且
,且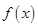 在
在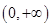 上单调递增.
上单调递增.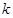 的值,并写出相应的函数
的值,并写出相应的函数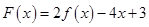 在区间
在区间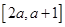 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;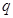 ,使函数
,使函数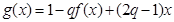 在区间
在区间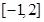 上的值域为
上的值域为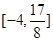 若存在,求出
若存在,求出