题目内容
如图,已知四棱锥P-ABCD的底面为菱形,且∠ABC =60°,AB=PC=2,AP=BP=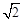 .
.
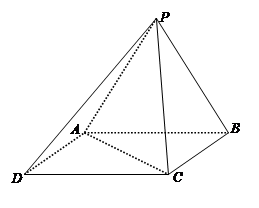
(Ⅰ)求证:平面PAB⊥平面ABCD ;
(Ⅱ)求二面角A-PC-D的平面角的余弦值.
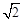 .
.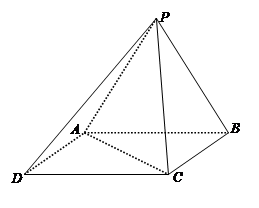
(Ⅰ)求证:平面PAB⊥平面ABCD ;
(Ⅱ)求二面角A-PC-D的平面角的余弦值.
(Ⅰ)见解析;(Ⅱ)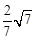 .
.
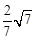 .
.试题分析:(Ⅰ)要证面面垂直,需在其中一面内找一条直线与另一面垂直,此题在面PAB内过点P向AB作垂线,在三角形PCE中,再根据边长关系证PE⊥CE,从而得证;(Ⅱ)法一:先找二面角的平面角,在Rt△PEC中,过点E作EF⊥PC于点F,连AF.过A作平面PCD的垂线,垂足为H,连FH,证
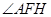 是二面角A-PC-D的平面角,再证
是二面角A-PC-D的平面角,再证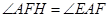 ,在
,在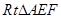 中,求
中,求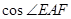 的值,即得所求;法二:以AB中点E为坐标原点,EC所在直线为x轴,EB所在直线为y轴,EP所在直线为z轴,建立如图所示的空间直角坐标系,写出各点空间坐标,设平面PAC与面PCD的法向量
的值,即得所求;法二:以AB中点E为坐标原点,EC所在直线为x轴,EB所在直线为y轴,EP所在直线为z轴,建立如图所示的空间直角坐标系,写出各点空间坐标,设平面PAC与面PCD的法向量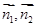 ,根据条件找和法向量垂直的已知向量列方程组求法向量,再利用
,根据条件找和法向量垂直的已知向量列方程组求法向量,再利用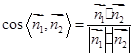 求法向量夹角的余弦值,即得所求.
求法向量夹角的余弦值,即得所求.试题解析:(Ⅰ)如图1所示,取AB中点E,连PE、CE.
则PE是等腰△PAB的底边上的中线,所以PE⊥AB. 2分
PE=1,CE=
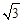 ,PC=2,即
,PC=2,即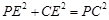 .
.由勾股定理可得,PE⊥CE. 4分
又因为ABÌ平面ABCD,CEÌ平面ABCD,
且AB∩CE=E,所以PE⊥平面ABCD. 5分
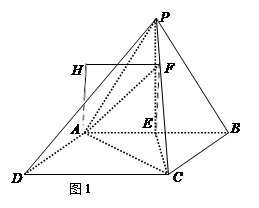
而PEÌ平面PAB,
所以平面PAB⊥平面ABCD. 7分
(Ⅱ)(方法1)如图1,在Rt△PEC中,过点E作EF⊥PC于点F,连AF.
过A作平面PCD的垂线,垂足为H,连FH.
因为AE⊥EC,AE⊥PE,所以AE⊥平面PEC,于是AE⊥PC.
又EF⊥PC,所以PC⊥平面AEF,故PC⊥AF.
已有PC⊥AH,可得PC⊥平面AFH,所以PC⊥FH.
故∠AFH是二面角A-PC-D的平面角. 10分
由AB⊥平面PEC知EF⊥AB,又AB∥CD,所以EF⊥CD.
而已有EF⊥PC,所以EF⊥平面PCD.又因为AH⊥平面PCD,所以AH∥EF.
由于AB∥平面PCD,所以A、E两点到平面PCD的距离相等,故AH=EF.
所以AEFH是矩形,∠AFH=∠EAF 13分
在Rt△AEF中,AE=1,EF=
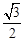 ,AF=
,AF=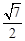 ,所以
,所以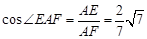 .
.即二面角A-PC-D的平面角的余弦值是
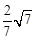 . 14分
. 14分(方法2)以AB中点E为坐标原点,EC所在直线为x轴,EB所在直线为y轴,EP所在直线为z轴,建立如图所示的空间直角坐标系.

则A(0,-1,0),C(
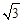 ,0,0),D(
,0,0),D(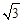 ,-2,0),P(0,0,1),
,-2,0),P(0,0,1),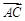 =(
=(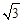 ,1,0),
,1,0),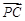 =(
=(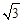 ,0,-1),
,0,-1),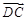 =(0,2,0). 9分
=(0,2,0). 9分设
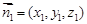 是平面PAC的一个法向量,
是平面PAC的一个法向量,则
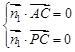 ,即
,即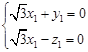 .
.取
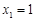 ,可得
,可得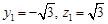 ,
,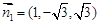 . 11分
. 11分设
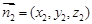 是平面PCD的一个法向量,则
是平面PCD的一个法向量,则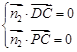 ,即
,即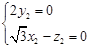 .
.取
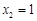 ,可得
,可得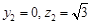 ,
,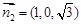 . 13分
. 13分故
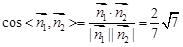 ,即二面角A-PC-D的平面角的余弦值是
,即二面角A-PC-D的平面角的余弦值是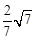 . 14分
. 14分
练习册系列答案
相关题目


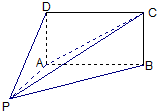
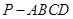 的底面
的底面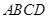 为矩形,且
为矩形,且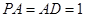 ,
,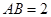 ,
,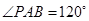 ,
,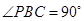 ,
,
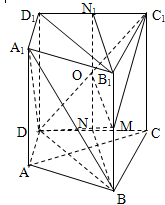
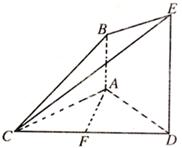
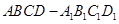 中,
中,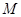 、
、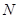 分别是
分别是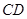 、
、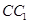 的中点,则异面直线
的中点,则异面直线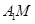 与
与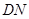 所成角的大小是( )
所成角的大小是( )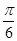
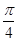
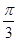
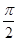
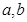 都在平面
都在平面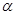 外, 则下列推断错误的是( )
外, 则下列推断错误的是( )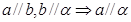
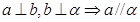
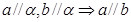
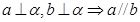
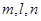 和平面
和平面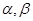 的四个命题:
的四个命题: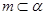 ,
,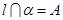 ,点
,点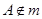 ,则
,则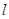 与
与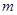 不共面;
不共面;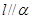 ,
,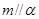 ,且
,且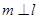 ,
,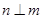 ,则
,则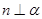 ;
;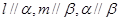 ,则
,则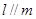 ;
;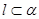 ,
,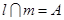 ,
,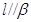 ,
,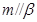 ,则
,则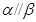 .
.