题目内容
（选做题）设函数f（x）=|x+1|+|x-a|．
（Ⅰ）若a=2，解不等式f（x）≥5；
（Ⅱ）如果?x∈R，f（x）≥3，求a的取值范围．
（Ⅰ）若a=2，解不等式f（x）≥5；
（Ⅱ）如果?x∈R，f（x）≥3，求a的取值范围．
分析：（I）当a=2，不等式即|x+1|+|x-2|≥5，根据绝对值的意义可得当x≤-2或x≥3时，|x+1|+|x-2|≥5成立，由此求得不等式的解集．
（II）若a=-1，f（x）=2|x+1|，不满足题设条件．若a＜-1，求得f（x）的最小值等于-1-a，若a＞-1，求得f（x）的最小值等于 1+a，根据f（x）≥3的充要条件是|a+1|≥3，求出a的取值范围．
（II）若a=-1，f（x）=2|x+1|，不满足题设条件．若a＜-1，求得f（x）的最小值等于-1-a，若a＞-1，求得f（x）的最小值等于 1+a，根据f（x）≥3的充要条件是|a+1|≥3，求出a的取值范围．
解答：解：（I）当a=2，f（x）=|x+1|+|x-2|，不等式f（x）≥5即|x+1|+|x-2|≥5．
而|x+1|+|x-2|表示数轴上的x对应点到-1、2对应点的距离之和，且-2和3对应点到-1、2对应点的距离之和正好等于5，
故当x≤-2或x≥3时，|x+1|+|x-2|≥5成立．
综上，不等式的解集为{x|x≤-2或x≥3}．（5分）
（II）若a=-1，f（x）=2|x+1|，不满足题设条件．
若a＜-1，f（x）=
，f（x）的最小值等于-1-a．
若a＞-1，
，f（x）的最小值等于 1+a．
所以?x∈R，f（x）≥3的充要条件是|a+1|≥3，故有a≤-4，或 a≥2，
从而a的取值范围是（-∞，-4]∪[2，+∞）．（10分）
而|x+1|+|x-2|表示数轴上的x对应点到-1、2对应点的距离之和，且-2和3对应点到-1、2对应点的距离之和正好等于5，
故当x≤-2或x≥3时，|x+1|+|x-2|≥5成立．
综上，不等式的解集为{x|x≤-2或x≥3}．（5分）
（II）若a=-1，f（x）=2|x+1|，不满足题设条件．
若a＜-1，f（x）=
|
若a＞-1，
|
所以?x∈R，f（x）≥3的充要条件是|a+1|≥3，故有a≤-4，或 a≥2，
从而a的取值范围是（-∞，-4]∪[2，+∞）．（10分）
点评：本题主要考查绝对值的意义，带有绝对值的函数，函数最值及其几何意义，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
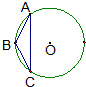短长度为
（三选一，考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）