题目内容
(2012•虹口区二模)在同一平面直角坐标系中,函数y=g(x)的图象与y=3x的图象关于直线y=x对称,而函数y=f(x)的图象与y=g(x)的图象关于y轴对称,若f(a)=-1,则a的值是
-
| 1 |
| 3 |
-
.| 1 |
| 3 |
分析:由函数y=g(x)的图象与y=3x的图象关于直线y=x对称,则y=g(x)的图象与y=3x互为反函数,易得y=g(x)的解析式,再由函数y=f(x)的图象与y=g(x)的图象关于y轴对称,进而可以得到函数y=f(x)的解析式,由函数y=f(x)的解析式构造方程f(a)=-1,解方程即可求也a的值.
解答:解:∵函数y=g(x)的图象与y=3x的图象关于直线y=x对称
∴函数y=g(x)与y=3x互为反函数
则g(x)=log3x,
又由y=f(x)的图象与y=g(x)的图象关于y轴对称
∴f(x)=log3(-x),
又∵f(a)=-1
∴log3(-a)=-1,
a=-
故答案为:-
.
∴函数y=g(x)与y=3x互为反函数
则g(x)=log3x,
又由y=f(x)的图象与y=g(x)的图象关于y轴对称
∴f(x)=log3(-x),
又∵f(a)=-1
∴log3(-a)=-1,
a=-
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
点评:本题主要考查了反函数,以及函数图象的性质,同时考查了图象的对称和对数的运算,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
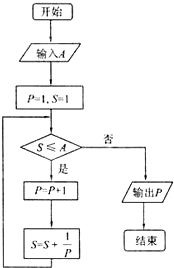 (2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为
(2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为