题目内容
7.在△ABC中,角A,B,C所对的边分别为Aa,b,c,且满足$\frac{c}{sinC}$=$\frac{a}{\sqrt{3}cosA}$(1)若4sinC=c2sinB,求△ABC的面积;
(2)若$\overrightarrow{AB}$$•\overrightarrow{BC}$+$\overrightarrow{A{B}^{2}}$=4,求a的最小值.
分析 (1)运用正弦定理和同角的商数关系,即可得到角A,再由三角形的面积公式,计算即可得到;
(2)运用向量的数量积的定义和向量的平方即为模的平方,由余弦定理和基本不等式,即可得到最小值.
解答 解:(1)由正弦定理,可得
$\frac{sinC}{sinC}$=$\frac{sinA}{\sqrt{3}cosA}$=1,
即有tanA=$\sqrt{3}$,
由0<A<π,可得A=$\frac{π}{3}$,
由正弦定理可得4c=bc2,即有bc=4,
△ABC的面积为S=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×4×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$;
(2)$\overrightarrow{AB}$$•\overrightarrow{BC}$+$\overrightarrow{A{B}^{2}}$=4,
可得c2-accosB=4,
由余弦定理,可得2c2-(a2+c2-b2)=8,
即b2+c2-a2=8,
又a2=b2+c2-2bccosA=b2+c2-bc,
即有bc=8,
由a2=b2+c2-bc≥2bc-bc=bc=8,
当且仅当b=c时,a取得最小值,且为2$\sqrt{2}$.
点评 本题考查正弦定理和余弦定理及面积公式的运用,考查向量的数量积的定义和性质,以及基本不等式的运用:求最值,属于中档题.

练习册系列答案
相关题目
2.函数y=ln(2x+5)的导函数f′(x)=( )
| A. | $\frac{1}{2x+5}$ | B. | $\frac{2}{2x+5}$ | C. | $\frac{5}{2x+5}$ | D. | $\frac{ln2}{2x+5}$ |
9.若一个命题的结论是“直线l在平面α内”,则用反证法证明这个命题时,第一步应作的假设为( )
| A. | 假设直线l∥平面α | B. | 假设直线l∩平面α于点A | ||
| C. | 假设直线l?平面α | D. | 假设直线l⊥平面α |
7.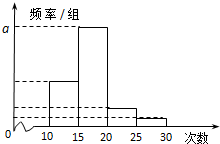 公司随机抽取M名员工作为样本,得到这M名员工参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
公司随机抽取M名员工作为样本,得到这M名员工参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(Ⅰ)求出表中M和图中a的值;
(Ⅱ)若该公司员工有240人,试估计员工参加社区服务的次数在区间[10,15)内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的员工中任选2人,求至多一人参加社区服务次数在区间[25,30)内的概率.
 公司随机抽取M名员工作为样本,得到这M名员工参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
公司随机抽取M名员工作为样本,得到这M名员工参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:(Ⅰ)求出表中M和图中a的值;
(Ⅱ)若该公司员工有240人,试估计员工参加社区服务的次数在区间[10,15)内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的员工中任选2人,求至多一人参加社区服务次数在区间[25,30)内的概率.
| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 24 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |