Question

10．已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=$\left\{{\begin{array}{l}{\frac{5}{4}sin\frac{π}{4}x，0≤x≤2}\\{{{（\frac{1}{2}）}^x}+1，x＞2}\end{array}}\right.$，若关于x的方程[f（x）]²+af（x）+b=0（a，b∈R），有且仅有6个不同实数根，则实数a的取值范围是（　　）

• A． （-$\frac{5}{2}$，-1）
• B． （-$\frac{5}{2}$，-$\frac{9}{4}$）
• C． （-$\frac{5}{2}$，-$\frac{9}{4}$）∪（-$\frac{9}{4}$，-1）
• D． （-$\frac{9}{4}$，-1）

Answer 1

分析 根据函数的奇偶性作出函数f（x）的图象，利用换元法判断函数t=f（x）的根的个数，利用数形结合即可得到结论．

解答 解：作出函数f（x）的图象如图：
则f（x）在（-∞，-2）和（0，2）上递增，在（-2，0）和（2，+∞）上递减，
当x=±2时，函数取得极大值f（2）=$\frac{5}{4}$；
当x=0时，取得极小值0．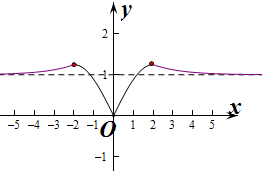

要使关于x的方程[f（x）]²+af（x）+b=0，a，b∈R有且只有6个不同实数根，
设t=f（x），则当t＜0，方程t=f（x），有0个根，
当t=0，方程t=f（x），有1个根，
当0＜t≤1或t=$\frac{5}{4}$，方程t=f（x），有2个根，
当1＜t＜$\frac{5}{4}$，方程t=f（x），有4个根，
当t＞$\frac{5}{4}$，方程t=f（x），有0个根．
则t²+at+b=0必有两个根t₁、t₂，
则有两种情况符合题意：
①t₁=$\frac{5}{4}$，且t₂∈（1，$\frac{5}{4}$），
此时-a=t₁+t₂，
则a∈（-$\frac{5}{2}$，-$\frac{9}{4}$）；
②t₁∈（0，1]，t₂∈（1，$\frac{5}{4}$），
此时同理可得a∈（-$\frac{9}{4}$，-1），
综上可得a的范围是（-$\frac{5}{2}$，-$\frac{9}{4}$）∪（-$\frac{9}{4}$，-1），
故选：C

点评 本题主要考查分段函数的应用，利用换元法结合函数奇偶性的对称性，利用数形结合是解决本题的关键．综合性较强．