题目内容
(本题13分)
设两个非零向量a与b不共线,
(1)若向量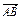 =a+b,
=a+b,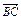 =2a+8b,
=2a+8b,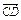 =3(a-b),求证:A、B、D三点共线;
=3(a-b),求证:A、B、D三点共线;
(2)试确定实数k,使向量ka+b和向量a+kb共线.
设两个非零向量a与b不共线,
(1)若向量
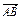 =a+b,
=a+b,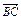 =2a+8b,
=2a+8b,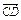 =3(a-b),求证:A、B、D三点共线;
=3(a-b),求证:A、B、D三点共线;(2)试确定实数k,使向量ka+b和向量a+kb共线.
(1)略
(2)
(1)证明 ∵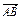 =a+b,
=a+b,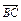 =2a+8b,
=2a+8b,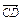 =3(a-b),
=3(a-b),
∴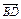 =
=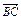 +
+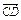 ="2a+8b+3(a-b)=2a+8b+3a-3b=5(a+b) " ………………2分
="2a+8b+3(a-b)=2a+8b+3a-3b=5(a+b) " ………………2分
=5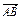 ………………4分
………………4分
∴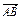 、
、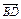 共线,
共线,  ………………5分
………………5分
又∵它们有公共点B,∴A、B、D三点共线. ………………6分
(2)解 ∵ka+b与a+kb共线,
∴存在实数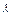 ,使ka+b=
,使ka+b=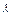 (a+kb), ……………8分
(a+kb), ……………8分
即ka+b=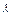 a+
a+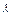 kb.
kb.
∴(k-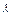 )a=(
)a=(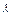 k-1)b ………………10分
k-1)b ………………10分
∵a、b是不共线的两个非零向量,
∴k-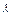 =
=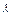 k-1=0,∴k2-1="0" ………………12分
k-1=0,∴k2-1="0" ………………12分
∴k=±1 ………………13分
………………13分
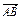 =a+b,
=a+b,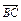 =2a+8b,
=2a+8b,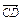 =3(a-b),
=3(a-b),∴
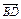 =
=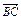 +
+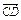 ="2a+8b+3(a-b)=2a+8b+3a-3b=5(a+b) " ………………2分
="2a+8b+3(a-b)=2a+8b+3a-3b=5(a+b) " ………………2分=5
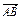 ………………4分
………………4分∴
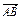 、
、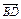 共线,
共线,  ………………5分
………………5分又∵它们有公共点B,∴A、B、D三点共线. ………………6分
(2)解 ∵ka+b与a+kb共线,
∴存在实数
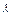 ,使ka+b=
,使ka+b=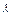 (a+kb), ……………8分
(a+kb), ……………8分即ka+b=
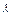 a+
a+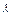 kb.
kb.∴(k-
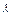 )a=(
)a=(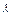 k-1)b ………………10分
k-1)b ………………10分∵a、b是不共线的两个非零向量,
∴k-
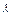 =
=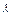 k-1=0,∴k2-1="0" ………………12分
k-1=0,∴k2-1="0" ………………12分∴k=±1
 ………………13分
………………13分
练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
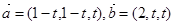 ,则
,则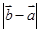 的最小值是 ( )
的最小值是 ( )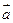
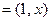 ,
,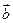
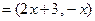
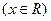 .
.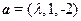 ,
,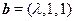 ,则
,则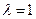 是
是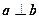 的 ▲ 条件.
的 ▲ 条件. 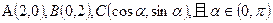 。
。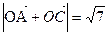 ,求
,求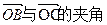 的余弦值。
的余弦值。
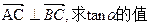 。
。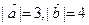 ,
,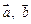 的夹角为60°,则
的夹角为60°,则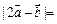 .
.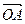 ="(1,1),"
="(1,1)," 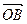 ="(1,-1),"
="(1,-1)," 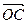 =(2cos
=(2cos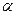 ,2sin
,2sin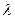 1,
1,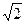 )2+
)2+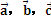 均为单位向量,且
均为单位向量,且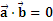 ,则
,则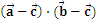 的最小值为 ( )
的最小值为 ( )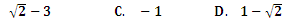
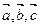 是任意的非零平面向量且互不共线,以下四个命题:
是任意的非零平面向量且互不共线,以下四个命题: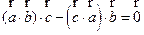 ;
;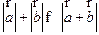 ;
; 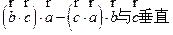 ;
;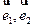 平行,则
平行,则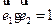 ;
;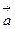 平移后得到y=2x+6的图象,
平移后得到y=2x+6的图象,