题目内容
【题目】定义 ![]() 为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为
为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为 ![]() ,又bn=
,又bn= ![]() ,则
,则 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:由已知定义,得到 ![]() =
= ![]() ,
,
∴a1+a2+…+an=n(2n+1)=Sn,
即Sn=2n2+n.
当n=1时,a1=S1=3.
当n≥2时,an=Sn﹣Sn﹣1=(2n2+n)﹣[2(n﹣1)2+(n﹣1)]=4n﹣1.
当n=1时也成立,
∴an=4n﹣1;
∵bn= ![]() =n,
=n,
∴ ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =1﹣
=1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =1﹣
=1﹣ ![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() ,
,
所以答案是:C
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系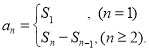 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目