题目内容
(本小题满分14分)
设 是定义在
是定义在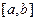 上的函数,用分点
上的函数,用分点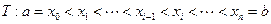
将区间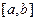 任意划分成
任意划分成 个小区间,如果存在一个常数
个小区间,如果存在一个常数 ,使得和式
,使得和式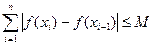 (
( )恒成立,则称
)恒成立,则称 为
为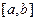 上的有界变差函数.
上的有界变差函数.
(1)函数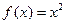 在
在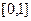 上是否为有界变差函数?请说明理由;
上是否为有界变差函数?请说明理由;
(2)设函数 是
是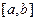 上的单调递减函数,证明:
上的单调递减函数,证明: 为
为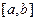 上的有界变差函数;
上的有界变差函数;
(3)若定义在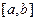 上的函数
上的函数 满足:存在常数
满足:存在常数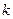 ,使得对于任意的
,使得对于任意的 、
、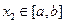 时,
时, .证明:
.证明: 为
为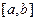 上的有界变差函数.
上的有界变差函数.
解:(1) 函数
函数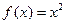 在
在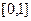 上是增函数,
上是增函数,  对任意划分
对任意划分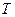 ,
,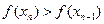
 ,
,
取常数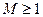 ,则和式
,则和式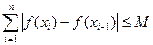 (
( )恒成立,
)恒成立,
所以函数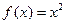 在
在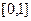 上是有界变差函数. …………4分
上是有界变差函数. …………4分
(2) 函数
函数 是
是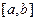 上的单调递减函数,
上的单调递减函数,
且对任意划分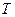 ,
,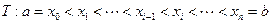
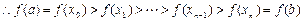
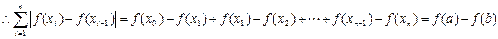 ,
,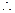 一定存在一个常数
一定存在一个常数 ,使
,使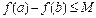 ,
,
故 为
为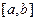 上的有界变差函数. …………9分
上的有界变差函数. …………9分
(3)

 对任意划分
对任意划分 ,
,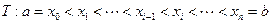
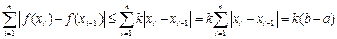 ,
,
取常数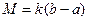 ,
,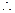 由有界变差函数定义知
由有界变差函数定义知 为
为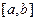 上的有界变差函数. …………14分
上的有界变差函数. …………14分
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
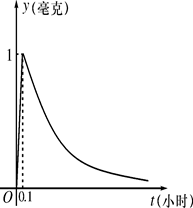
(本小题满分12分) 为了预防流感,某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第
为了预防流感,某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第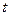 小时教室内每立方米空气中的含药量为
小时教室内每立方米空气中的含药量为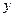 毫克.已知药物释放过程中,教室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
毫克.已知药物释放过程中,教室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为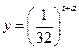 (a为常数).函数图象如图所示.
(a为常数).函数图象如图所示.
根据图中提供的信息,解答下列问题:
(1)求从药物释放开始每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
|
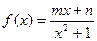 为奇函数且
为奇函数且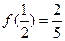
 上是增函数。
上是增函数。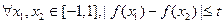 恒成立,求t的最小值。
恒成立,求t的最小值。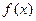 对任意
对任意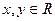 都有
都有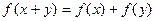 且x>0时,
且x>0时,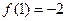 .(1)求
.(1)求 ,(其中
,(其中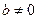 )
)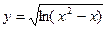
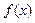 在其定义域上满足
在其定义域上满足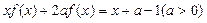 .
.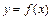 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);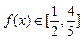 时,求x的取值范围;
时,求x的取值范围;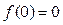 ,数列
,数列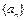 满足
满足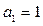 ,那么:
,那么: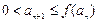 ,正整数N满足
,正整数N满足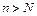 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列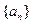 ,
, 恒成立,求最小的N;
恒成立,求最小的N;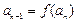 ,求证:
,求证: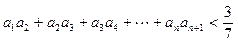 .
.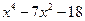 (2)
(2)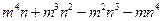
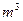 ,深为3
,深为3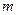 .如果池底每平方米的造价为150元,池壁每平方米的造价为
.如果池底每平方米的造价为150元,池壁每平方米的造价为 120元,怎样设计水池能使总造价最低?最低造价是多少?
120元,怎样设计水池能使总造价最低?最低造价是多少?