题目内容
19.设函数y=f(x)(x∈R,且x≠0)对任意的非零实数x,y,都有f(xy)=f(x)+f(y)成立.(1)求证:f(1)=f(-1)=0,且f($\frac{1}{x}$)=-f(x)(x≠0);
(2)判断f(x)的奇偶性;
(3)若f(x)在(0,+∞)上单调递增,解不等式f($\frac{1}{x}$)-f(2x-1)≥0.
分析 (1)赋值x=y=1,x=y=-1,y=$\frac{1}{x}$,即可证明结论;
(2)令y=-1,可得f(-x)=f(x)+f(-1)=f(x),即可判断f(x)的奇偶性;
(3)f($\frac{1}{x}$)-f(2x-1)≥0,f(x)在(0,+∞)上单调递增,f(x)是偶函数,可得|$\frac{1}{x}$|≥|2x-1|,即可得出结论.
解答 (1)证明:令x=y=1,可得f(1)=f(1)+f(1),∴f(1)=0,
令x=y=-1,可得f(1)=f(-1)+f(-1),∴f(-1)=0,
令y=$\frac{1}{x}$,可得f(1)=f(x)+f($\frac{1}{x}$),∴f($\frac{1}{x}$)=-f(x)(x≠0);
(2)解:令y=-1,可得f(-x)=f(x)+f(-1)=f(x),
∴函数f(x)是偶函数;
(3)解:∵f($\frac{1}{x}$)-f(2x-1)≥0,
∴f($\frac{1}{x}$)≥f(2x-1),
∵f(x)在(0,+∞)上单调递增,f(x)是偶函数
∴|$\frac{1}{x}$|≥|2x-1|,
∴-1≤x(2x-1)≤1,
∴-$\frac{1}{2}$≤x≤1,
∵x≠0,2x-1≠0
∴不等式的解集为{x|-$\frac{1}{2}$≤x≤1且x$≠0,x≠\frac{1}{2}$}.
点评 本题考查赋值法的运用,考查函数的奇偶性,考查解不等式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
9.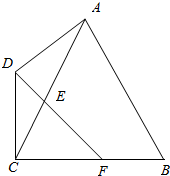 如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
 如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{3}{4}$ | D. | -1 |
8.甲乙两人相约打靶,甲射击3次,每次射击的命中率为$\frac{1}{2}$,乙射击2次,每次射击的命中率为$\frac{2}{3}$,记甲命中的次数为x,乙命中的次数为y
(1)求x+y的分布列和E(x+y)
(2)猜想两个相互独立的变量x,y的期望与x+y的期望间的关系,并证明你的猜想.
其中,x的分布列为:
y的分布列为:
(1)求x+y的分布列和E(x+y)
(2)猜想两个相互独立的变量x,y的期望与x+y的期望间的关系,并证明你的猜想.
其中,x的分布列为:
| x | x1 | x2 | … | xn |
| p | p1 | p2 | pn |
| y | y1 | y2 | … | ym |
| p | p${\;}_{1}^{′}$ | p${\;}_{2}^{′}$ | … | p${\;}_{m}^{′}$ |
 在△ABC中,P为AB的中点,O在边AC上,且|$\overrightarrow{AO}$|=2|$\overrightarrow{OC}$|,BO∩CP=R,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
在△ABC中,P为AB的中点,O在边AC上,且|$\overrightarrow{AO}$|=2|$\overrightarrow{OC}$|,BO∩CP=R,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.