��Ŀ����
����Ŀ������ƽ��ֱ������ϵxOy�У���֪����C1��x2+y2=1����ƽ��ֱ������ϵxOy��ԭ��OΪ���㣬x���������Ϊ���ᣬȡ��ͬ�ĵ�λ���Ƚ���������ϵ����ֱ֪��l���ѣ�2cos�ȩ�sin�ȣ�=6��
��1��������C1�ϵ����е�ĺ����ꡢ������ֱ��쳤Ϊԭ���� ![]() ��2����õ�����C2 �� ��д��ֱ��l��ֱ�����귽�̺�����C2�IJ������̣�
��2����õ�����C2 �� ��д��ֱ��l��ֱ�����귽�̺�����C2�IJ������̣�
��2��������C2����һ��P��ʹ��P��ֱ��l�ľ��������������ֵ��
���𰸡�
��1���⣺�������֪��ֱ��l��ֱ�����귽��Ϊ��2x��y��6=0��
��Ϊ����C2��ֱ�����귽��Ϊ�� ![]() ��
��
������C2�IJ��������� ![]() ����������
����������
��2���⣺��P�����꣨ ![]() �������P��ֱ��l�ľ���Ϊ��
�������P��ֱ��l�ľ���Ϊ��
![]() =
= ![]() ��
��
�൱sin��60�㩁�ȣ�=��1ʱ����P�� ![]() ����
����
��ʱ ![]()
����������1��ֱ��д��ֱ��l��ֱ�����귽�̣�������C1�ϵ����е�ĺ����ꡢ������ֱ��쳤Ϊԭ���� ![]() ��2����õ�����C2�ķ��̣�Ȼ��д������C2�IJ������̣���2���������C2��һ��P�����꣬���õ�P��ֱ��l�ľ��빫ʽ������������ʽ���������DZ任������ֵ��
��2����õ�����C2�ķ��̣�Ȼ��д������C2�IJ������̣���2���������C2��һ��P�����꣬���õ�P��ֱ��l�ľ��빫ʽ������������ʽ���������DZ任������ֵ��
�����㾫����ͨ��������õ㵽ֱ�ߵľ��빫ʽ�����յ�![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ��
�ľ���Ϊ��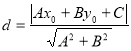 �����Խ����⣮
�����Խ����⣮


