题目内容
直线l: x-2y+2=0过椭圆的左焦点F和一个顶点B, 则该椭圆的离心率为( )
A.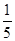 | B. | C.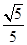 | D.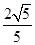 |
D
分析:分别令直线方程中y=0和x=0,进而求得b和c,进而根据b,c和a的关系求得a,则椭圆的离心率可得.
解答:解:在l:x-2y+2=0上,
令y=0得F1(-2,0),
令x=0得B(0,1),即c=2,b=1.
∴a=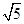 ,e=
,e=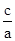 =
= .
.
故选D
解答:解:在l:x-2y+2=0上,
令y=0得F1(-2,0),
令x=0得B(0,1),即c=2,b=1.
∴a=
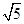 ,e=
,e=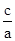 =
= .
.故选D

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 (
(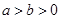 )的左焦点
)的左焦点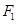 作
作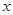 轴的垂线交椭圆于
轴的垂线交椭圆于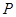 、
、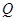 两点,
两点,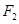 为右焦点,若
为右焦点,若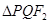 为等边三角形,则椭圆的离心率为( )
为等边三角形,则椭圆的离心率为( )



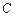 :+=1(a>b>0)的长轴AB长为4,离心率e=,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连结AQ延长交直线
:+=1(a>b>0)的长轴AB长为4,离心率e=,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连结AQ延长交直线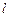 于点M,N为
于点M,N为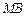 的中点.
的中点.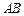 为直径的圆
为直径的圆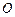 上;
上;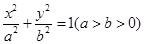 的右焦点
的右焦点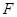 ,直线
,直线 与
与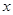 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点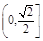
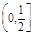
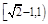
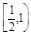
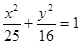 的焦点为顶点,离心率为
的焦点为顶点,离心率为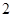 的双曲线方程( )
的双曲线方程( )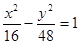

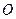 ,焦点在
,焦点在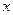 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为 一个正方形的顶点.过右焦点
一个正方形的顶点.过右焦点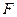 与
与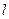 交椭圆于
交椭圆于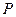 ,
,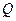 两点.
两点. 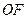 上是否存在点
上是否存在点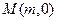 ,使得以
,使得以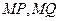 为邻边的平行四边形是菱形? 若存在,求出
为邻边的平行四边形是菱形? 若存在,求出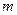 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.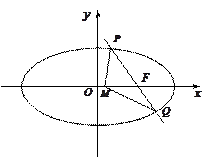
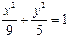 的中心为顶点,左准线为准线的抛物线方程是 .
的中心为顶点,左准线为准线的抛物线方程是 .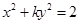 表示焦点在y轴上的椭圆,则k的取值范围是 ( )
表示焦点在y轴上的椭圆,则k的取值范围是 ( )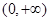
 的离心率为
的离心率为