题目内容
函数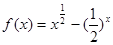 的零点个数为( )
的零点个数为( )
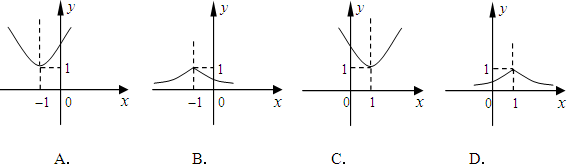
| A.0 | B.1 | C.2 | D.3 |
B
解析试题分析:在同一坐标系中,分别画出函数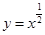 和函数
和函数 的图象,可以看出两函数的图象只有一个交点,所以函数
的图象,可以看出两函数的图象只有一个交点,所以函数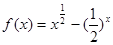 只有一个零点.
只有一个零点.
考点:本小题主要考查函数零点的概念和数形结合判断零点的个数,考查学生的转化能力.
点评:当一个函数中含有两种以上函数类型时,直接求解往往行不通,这时需要画出函数的图象,数形结合判断函数的零点的个数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数 的单调递减区间是 ( )
的单调递减区间是 ( )
A. | B.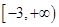 | C. | D. |
函数f (x)=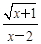 的定义域为
的定义域为
| A.[-1,2)∪(2,+∞) | B.(-∞,+∞) |
| C.[-1,+∞) | D.(-∞,2)∪(2,+∞) |
已知函数唯一的零点在区间(1,3),(1,4),(1,5)内,那么下列命题不正确的是
| A.函数f (x)在区间(1,2)或[2,3)内有零点 |
| B.函数f (x)在(3,5)内无零点 |
| C.函数f (x)在(2,5)内一定有零点 |
| D.函数f (x)在(2,4)内不一定有零点 |
函数 的零点所在的一个区间是
的零点所在的一个区间是
A. | B.(1,2) | C.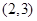 | D.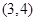 |
设f(x)是R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=
| A.3 | B.1 | C.-1 | D.-3 |
函数 的值域是 ( )
的值域是 ( )
A.(- ) ) | B.(-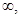 0) 0)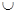 (0,+ (0,+ ) ) |
C.(-1,+ ) ) | D.(- ,-1) ,-1)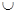 (0,+ (0,+ ) ) |
 是定义在[-6,6]上的偶函数,且
是定义在[-6,6]上的偶函数,且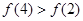 ,则下列各式一定成立的是( )
,则下列各式一定成立的是( )
A.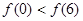 | B.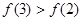 |
C.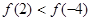 | D.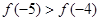 |
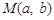 在直线
在直线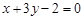 上,则当
上,则当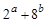 取得最小值时,函数
取得最小值时,函数 的图象大致为( )
的图象大致为( )