题目内容
9.计算:(1)$\frac{1-{a}^{-\frac{1}{2}}}{1+{a}^{-\frac{1}{2}}}$-$\frac{2{a}^{\frac{1}{2}}}{a-1}$;
(2)2${\;}^{3+lo{g}_{2}5}$;
(3)lg5•lg20+(lg2)2.
分析 (1)利用有理指数幂求解即可.
(2)(3)利用对数的运算法则求解即可.
解答 解:(1)$\frac{1-{a}^{-\frac{1}{2}}}{1+{a}^{-\frac{1}{2}}}$-$\frac{2{a}^{\frac{1}{2}}}{a-1}$=$\frac{(1-{a}^{-\frac{1}{2}})^{2}}{(1+{a}^{-\frac{1}{2}})(1-{a}^{-\frac{1}{2}})}$-$\frac{2{a}^{\frac{1}{2}}}{a-1}$=$\frac{1-2{a}^{-\frac{1}{2}}+{a}^{-1}}{1-{a}^{-1}}+\frac{2{a}^{\frac{1}{2}}}{1-a}$=$\frac{1-2{a}^{\frac{1}{2}}+a}{a-1}-\frac{2{a}^{\frac{1}{2}}}{a-1}$$\frac{1+a}{a-1}$=
(2)2${\;}^{3+lo{g}_{2}5}$=8•${2}^{{log}_{2}5}$=40.
(3)lg5•lg20+(lg2)2=2lg5•lg2+(lg5)2+(lg2)2=(lg2+lg5)2=1
点评 本题考查对数的运算法则的应用,有理指数幂的化简求值,考查计算能力.

练习册系列答案
相关题目
18.已知四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F是棱PC、PD的中点,则:①AB⊥PD;②平面PBC与平面ABCD垂直;③△PCD的面积大于△PAB的面积;④直线AE与直线BF是异面直线.其中正确结论的序号是( )
| A. | ①② | B. | ①④ | C. | ②④ | D. | ①③ |
19.若a是实数,则“a2≠9”是“a≠3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
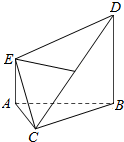 在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE.
在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE.