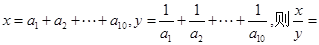题目内容
(13分)一个同心圆形花坛,分为两部分,中间小圆部分种植绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
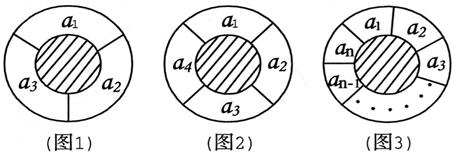
⑴ 如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?
如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
⑵ 如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?
⑴ 如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?
如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
⑵ 如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?

)⑴如图1,先对a1部分种植,有3种不同的种法,再对a2、a3种植,
因为a2、a3与a1不同颜色,a2、a3也不同。 所以S(3)=3×2=6(种)。
如图2,S(4)=3×2×2×2-S(3)=18(种)。
⑵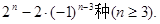
因为a2、a3与a1不同颜色,a2、a3也不同。 所以S(3)=3×2=6(种)。
如图2,S(4)=3×2×2×2-S(3)=18(种)。
⑵
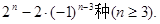
本试题主要考查了排列组合的运用,解决实际问题,同时也考查了数列的求和的运用,数列的概念的综合试题。
(1)先对a1部分种植,有3种不同的种法,再对a2、a3种植,
因为a2、a3与a1不同颜色,a2、a3也不同。 所以S(3)=3×2=6(种)。………3分
如图2,S(4)=3×2×2×2-S(3)=18(种)
(2)圆环分为n等份,对a1有3种不同的种法,对a2、a3、…、an都有两种不同的种法,但这样的种法只能保证a1与ai(i=2、3、……、n-1)不同颜色,但不能保证a1与an不同颜色.
于是一类是an与a1不同色的种法,这是符合要求的种法,记为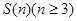 种. 另一类是an与a1同色的种法,这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为
种. 另一类是an与a1同色的种法,这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为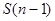 .共有3×2n-1种种法
.共有3×2n-1种种法
因此可得到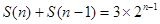 ,进而分析求解。
,进而分析求解。
)⑴如图1,先对a1部分种植,有3种不同的种法,再对a2、a3种植,
因为a2、a3与a1不同颜色,a2、a3也不同。 所以S(3)=3×2=6(种)。………3分
如图2,S(4)=3×2×2×2-S(3)=18(种)。………………………………………6分
⑵如图3,圆环分为n等份,对a1有3种不同的种法,对a2、a3、…、an都有两种不同的种法,但这样的种法只能保证a1与ai(i=2、3、……、n-1)不同颜色,但不能保证a1与an不同颜色.
于是一类是an与a1不同色的种法,这是符合要求的种法,记为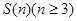 种. 另一类是an与a1同色的种法,这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为
种. 另一类是an与a1同色的种法,这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为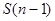 .
.
共有3×2n-1种种法.………………………………………………………………9分
这样就有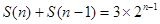 .即
.即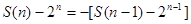 ,
,
则数列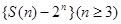 是首项为
是首项为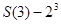 公比为-1的等比数列.……………10分
公比为-1的等比数列.……………10分
则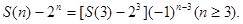
由⑴知: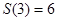 ,∴
,∴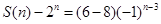 .
.
∴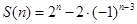 .………………………………………………………12分
.………………………………………………………12分
答:符合要求的不同种法有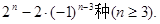 ……………………………13分
……………………………13分
(1)先对a1部分种植,有3种不同的种法,再对a2、a3种植,
因为a2、a3与a1不同颜色,a2、a3也不同。 所以S(3)=3×2=6(种)。………3分
如图2,S(4)=3×2×2×2-S(3)=18(种)
(2)圆环分为n等份,对a1有3种不同的种法,对a2、a3、…、an都有两种不同的种法,但这样的种法只能保证a1与ai(i=2、3、……、n-1)不同颜色,但不能保证a1与an不同颜色.
于是一类是an与a1不同色的种法,这是符合要求的种法,记为
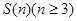 种. 另一类是an与a1同色的种法,这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为
种. 另一类是an与a1同色的种法,这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为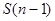 .共有3×2n-1种种法
.共有3×2n-1种种法因此可得到
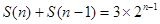 ,进而分析求解。
,进而分析求解。)⑴如图1,先对a1部分种植,有3种不同的种法,再对a2、a3种植,
因为a2、a3与a1不同颜色,a2、a3也不同。 所以S(3)=3×2=6(种)。………3分
如图2,S(4)=3×2×2×2-S(3)=18(种)。………………………………………6分
⑵如图3,圆环分为n等份,对a1有3种不同的种法,对a2、a3、…、an都有两种不同的种法,但这样的种法只能保证a1与ai(i=2、3、……、n-1)不同颜色,但不能保证a1与an不同颜色.
于是一类是an与a1不同色的种法,这是符合要求的种法,记为
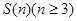 种. 另一类是an与a1同色的种法,这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为
种. 另一类是an与a1同色的种法,这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为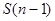 .
.共有3×2n-1种种法.………………………………………………………………9分
这样就有
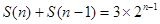 .即
.即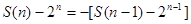 ,
,则数列
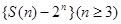 是首项为
是首项为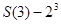 公比为-1的等比数列.……………10分
公比为-1的等比数列.……………10分则
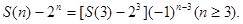
由⑴知:
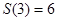 ,∴
,∴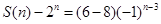 .
.∴
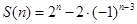 .………………………………………………………12分
.………………………………………………………12分答:符合要求的不同种法有
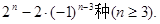 ……………………………13分
……………………………13分
练习册系列答案
相关题目
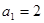 ,点
,点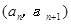 在函数
在函数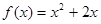 的图象上,其中
的图象上,其中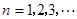
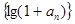 是等比数列;
是等比数列;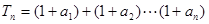 ,求
,求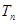 ;
;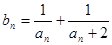 ,求数列
,求数列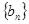 的前n项和为Sn,并证明Sn<1
的前n项和为Sn,并证明Sn<1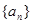 满足
满足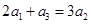 ,且
,且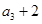 是
是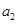 与
与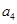 的等差中项;
的等差中项;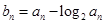 ,
,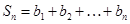 ,
,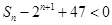 成立的
成立的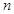 的最小值;
的最小值; 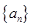 中,
中,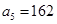 ,公比
,公比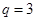 ,前
,前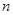 项和
项和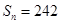 ,求首项
,求首项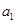 和项数
和项数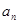 }的前n项和为
}的前n项和为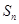 ,若
,若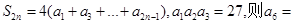
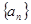 中,
中,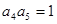 ,
,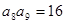 ,则
,则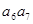 等于( )
等于( )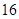
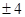
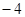
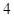
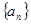 中,
中, 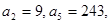 则
则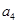 = ( )
= ( )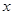 ,
,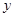 ,
,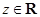 ,若
,若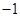 ,
,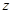 ,
,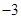 成等比数列,则
成等比数列,则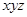 的值为
的值为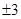
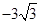
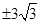
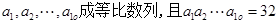 记
记