题目内容
【题目】已知双曲线C1的渐近线是
x±2y=0，焦点坐标是F1（-
，0）、F2（，0）．
（1）求双曲线C1的方程；
（2）若椭圆C2与双曲线C1有公共的焦点，且它们的离心率之和为
，点P在椭圆C2上，且|PF1|=4，求∠F1PF2的大小．
【答案】（1）
（2）120°
【解析】
（1）设双曲线C1：
，由已知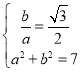
，由此能求出双曲线C1方程．
（2）由已知得椭圆C2离心率是
，
，a=3，
，由此利用余弦定理能求出∠F1PF2的大小．
解：（1）根据题意，设双曲线C1：，
则，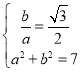
，
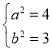双曲线C1方程是
．
（2）∵双曲线C1的离心率是
，∴椭圆C2离心率是，
在椭圆C2中，，∴a=3，，
∵|PF1|=4，由椭圆定义，|PF2|=2，在△F1PF2中，
根据余弦定理，
，
∴∠F1PF2=120°．
练习册系列答案
阅读快车系列答案
相关题目
【题目】为了解某班学生喜好体育运动是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知按喜好体育运动与否，采用分层抽样法抽取容量为10的样本，则抽到喜好体育运动的人数为6.
（1）请将上面的列联表补充完整；
（2）能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关？说明理由.
附：
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
