��Ŀ����
����Ŀ��ij���쳧��10�·�������һ��ƹ�����������ȡ![]() �����м�飬���ÿ�����ֱ������λ��
�����м�飬���ÿ�����ֱ������λ��![]() ���������ݽ��з��飬�õ�����Ƶ�ʷֲ�����
���������ݽ��з��飬�õ�����Ƶ�ʷֲ�����

��1����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ֵ��������Ƶ�ʷֲ�ֱ��ͼ�����������λС������
��ֵ��������Ƶ�ʷֲ�ֱ��ͼ�����������λС������
��2����֪��ƹ�����ֱ��Ϊ![]() ��ֱ��������
��ֱ��������![]() ��Ϊ����ƹ����������ƹ������
��Ϊ����ƹ����������ƹ������![]() �����Թ�����������ƹ�������Ŀ��
�����Թ�����������ƹ�������Ŀ��
��3��ͳ�Ʒ����У�ͬһ�����ݳ��ø���������е�ֵ����������![]() ���е�ֵ��
���е�ֵ��![]() ����Ϊ��������������ƹ����ֱ����ƽ��ֵ����λ����
����Ϊ��������������ƹ����ֱ����ƽ��ֵ����λ����
���𰸡���1��![]() ��Ƶ�ʷֲ�ֱ��ͼ����������2��
��Ƶ�ʷֲ�ֱ��ͼ����������2��![]() ����3��
����3��![]() ��
��![]() ��
��
���������������: ��1������Ƶ�ʵ���Ƶ��������������������![]() ������
������![]() ��ӦƵ��
��ӦƵ��![]() ������Ƶ����Ϊ������
������Ƶ����Ϊ������![]() ������ٸ���Ƶ�ʵ���Ƶ��������������
������ٸ���Ƶ�ʵ���Ƶ��������������![]() ��
��![]() ��ֵ����Ƶ�ʳ��������Ϊ��Ӧ���������껭��Ƶ�ʷֲ�ֱ��ͼ����2��ֱ����
��ֵ����Ƶ�ʳ��������Ϊ��Ӧ���������껭��Ƶ�ʷֲ�ֱ��ͼ����2��ֱ����![]() �ڶ�Ӧ����Ϊ
�ڶ�Ӧ����Ϊ![]() ������Ƶ��������������Ƶ�ʣ���Ƶ������3����ƽ��ֵΪ�����е�ֵ���Ӧ���ʳ˻��ĺͣ���ƽ��ֵ����λ����������
������Ƶ��������������Ƶ�ʣ���Ƶ������3����ƽ��ֵΪ�����е�ֵ���Ӧ���ʳ˻��ĺͣ���ƽ��ֵ����λ����������![]() �ڣ���Ƶ�ʹ�ϵ�е�����ϵ������λ��Ϊ
�ڣ���Ƶ�ʹ�ϵ�е�����ϵ������λ��Ϊ![]() ������
������![]() ���ⷽ�̿ɵ���λ��.
���ⷽ�̿ɵ���λ��.
�������:��1����Ƶ�ʷֲ�����֪![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
Ƶ�ʷֲ�ֱ��ͼ��ͼ��
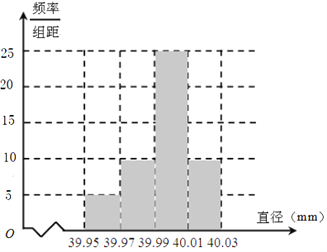
��2����Ϊ����ƹ�����ֱ����![]() �ڣ�������Ƶ�ʷֲ������ɵ�����ƹ�����Ƶ��Ϊ
�ڣ�������Ƶ�ʷֲ������ɵ�����ƹ�����Ƶ��Ϊ![]() ����6�֣�
����6�֣�
��![]() ��ƹ�����У�������ƹ��������Լ��
��ƹ�����У�������ƹ��������Լ��![]() ��������
��������
��3��ƽ����![]() .
.
����λ��Ϊ![]() ����
����![]() ��
��![]() �����
�����![]() .����λ��Ϊ
.����λ��Ϊ![]() ��
��

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�����Ŀ��ijѧУһ��������ȤС���ѧУ���˹�������ֳ��ij��������й۲��о��������ϳ����ǰ���£���ȤС�������ʱ��x(��λ����)�����������ƽ������y(��λ��ǧ��)�õ�һ��۲�ֵ�����±���
|
|
|
|
|
|
|
|
|
|
|
|
(1)�ڸ���������ϵ�У���������x��y������ر�����ɢ��ͼ��
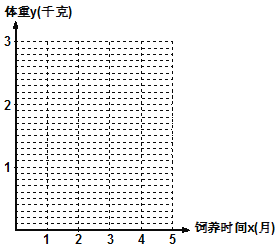
(2)������ϱ��ṩ�����ݣ�����С���˷��������![]() ���ڱ���
���ڱ���![]() �����Իع�ֱ�߷���
�����Իع�ֱ�߷���![]() ��
��
(3)Ԥ��������12����ʱ���������ƽ������(��λ��ǧ��)��
���ο���ʽ�� 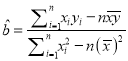 ��
�� ![]() ��
��


