题目内容
过抛物线y2=2px（p＞0）的焦点F作倾斜角为450的直线，交抛物线于A，B两点，若|AB|=4，则p的值为
- A.1
- B.2
- C.3
- D.4
A
分析：设出直线的方程，与抛物线的方程联立消去y，进而根据韦达定理表示出x1+x2和x1x2，进而利用配方法求得|x1-x2|，利用弦长公式表示出AB的长，即可求得p．
解答：由题意可知过焦点的直线方程为y=x-
，代入抛物线y2=2px，
消去y可得x2-3px+
=0，
设A（x1，y1），B（x2，y2），则
∴x1+x2=3p，x1x2=．
∴|AB|=
|x1-x2|=•
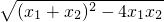=4p=4
解得p=1
故选A．
点评：本题主要考查了抛物线的简单性质．涉及直线与抛物线的关系时，往往是利用韦达定理设而不求．
分析：设出直线的方程，与抛物线的方程联立消去y，进而根据韦达定理表示出x1+x2和x1x2，进而利用配方法求得|x1-x2|，利用弦长公式表示出AB的长，即可求得p．
解答：由题意可知过焦点的直线方程为y=x-
，代入抛物线y2=2px，消去y可得x2-3px+
=0，设A（x1，y1），B（x2，y2），则
∴x1+x2=3p，x1x2=
．∴|AB|=
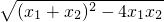|x1-x2|=•=4p=4解得p=1
故选A．
点评：本题主要考查了抛物线的简单性质．涉及直线与抛物线的关系时，往往是利用韦达定理设而不求．
练习册系列答案
阅读快车系列答案
相关题目
过抛物线y2=2px（p＞0）的焦点F的直线l与抛物线在第一象限的交点为A，与抛物线的准线的交点为B，点A在抛物线准线上的射影为C，若
=
，
•
=48，则抛物线的方程为（ ）
| AF |
| FB |
| BA |
| BC |
| A、y2=4x | ||
| B、y2=8x | ||
| C、y2=16x | ||
D、y2=4
|
过抛物线y2=2px（p＞0）的焦点F作直线交抛物线于A、B两点，O为抛物线的顶点．则△ABO是一个（ ）
| A、等边三角形 | B、直角三角形 | C、不等边锐角三角形 | D、钝角三角形 |