题目内容
【题目】已知椭圆![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为6,且面积的最大值为
的周长为6,且面积的最大值为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过
,过![]() ,
,![]() 分别作直线
分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() .若
.若![]() ,
,![]() ,
,![]() 的面积成等差数列,求直线
的面积成等差数列,求直线![]() 斜率的取值范围.
斜率的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题意列关于a,b的方程组,即可得到![]() 的方程;
的方程;
(2) 设直线![]() 的方程为
的方程为![]() ,联立方程可得
,联立方程可得![]() ,利用韦达定理表示条件
,利用韦达定理表示条件![]() ,以
,以![]() ,进而得到直线
,进而得到直线![]() 斜率的取值范围.
斜率的取值范围.
(1)因为![]() 是
是![]() 上的点,且
上的点,且![]() ,
,![]() 为
为![]() 的左、右焦点,所以
的左、右焦点,所以![]() ,
,
又因为![]() ,
,![]() 的周长为6,
的周长为6,
所以![]() ,
,
当![]() 为短轴端点时,
为短轴端点时,![]() 的面积最大,
的面积最大,
所以![]() ,
,
又因为![]() ,解得
,解得![]() ,
,![]() ,
,![]() ,
,
所以![]() 的方程为
的方程为![]() .
.
(2)依题意,直线![]() 与
与![]() 轴不重合,故可设直线
轴不重合,故可设直线![]() 的方程为
的方程为![]() ,
,
由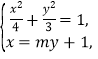 消去
消去![]() 得:
得:![]() ,
,
设![]() ,
,![]() ,则有
,则有![]() 且
且![]() ,
,![]() .
.
设![]() ,
,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() 成等差数列,所以
成等差数列,所以![]() ,即
,即![]() ,
,
则![]()
![]() ,
,
即![]() ,得
,得![]() ,
,
又![]() ,
,![]() ,于是
,于是![]() ,
,
所以![]() ,由
,由![]() 得
得![]() ,解得
,解得![]() ,
,
设直线![]() 的斜率为
的斜率为![]() ,则
,则![]() ,所以
,所以![]() ,
,
解得![]() 或
或![]() ,
,
所以直线![]() 斜率的取值范围是
斜率的取值范围是![]() .
.

 阅读快车系列答案
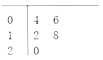
阅读快车系列答案【题目】近年来,我国工业经济发展迅速,工业增加值连年攀升,某研究机构统计了近十年(从2008年到2017年)的工业增加值(万亿元),如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
工业增加值 | 13.2 | 13.8 | 16.5 | 19.5 | 20.9 | 22.2 | 23.4 | 23.7 | 24.8 | 28 |
依据表格数据,得到下面的散点图及一些统计量的值.
|
|
|
|
|
5.5 | 20.6 | 82.5 | 211.52 | 129.6 |
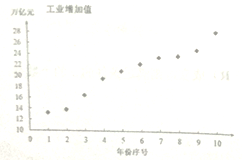
(1)根据散点图和表中数据,此研究机构对工业增加值![]() (万亿元)与年份序号
(万亿元)与年份序号![]() 的回归方程类型进行了拟合实验,研究人员甲采用函数
的回归方程类型进行了拟合实验,研究人员甲采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员乙采用函数
;研究人员乙采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员丙采用线性函数
;研究人员丙采用线性函数![]() ,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数
,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数![]() 与拟合指数
与拟合指数![]() 满足关系
满足关系![]() ).
).
(2)根据(1)的判断结果及统计值,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)预测到哪一年的工业增加值能突破30万亿元大关.
附:样本![]()
![]() 的相关系数
的相关系数 ,
,
![]() ,
,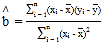 ,
,![]() .
.