题目内容
【题目】最近的一次数学竞赛共6道试题，每题答对得7分，答错(或不答)得0分.赛后某参赛代表队获团体总分161分，且统计分数时发现：该队任两名选手至多答对两道相同的题目.没有三名选手都答对两道相同的题目.试问该队选手至少有多少人？
【答案】7
【解析】
设该队有n名选手，分别记为
，记6道题的编号依次为1,2,...,6.以编号为行、选手为列作一个6×n的方格表.如果选手
答对第j(j=1,2,...,6)题，就将方格表中第j行第i列的小方格(j, i)的中心染成红点.我们的问题就是在6×n的方格表中，不存在“横”6点矩形
和“纵”6点矩形
的情况，且至少有23个红点时，求n的最小值.
如第1列有6个红点，那么，后面各列至多有2个红点.因为
，于是，取第2至10列，其中第2至9列每列有2个红点，第10列1个红点(如图)满足题设.这说明n的最小值不大于10.
我们发现，可通过将第1列中某点移到此点所在行的其他列中来减少图6的列数，如作移动(6, 1)→(6,2)，可同时作移动(4,10)→(6,3)，(3,9)→(6,4)，(5,9)→(6,7)，这样便得到有23个红点的图7.类似地可得图8.这说明n的最小值不大于7.
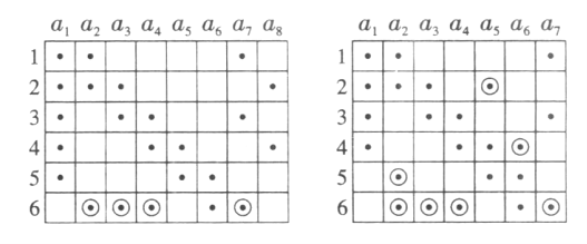
下面证明：n的最小值大于6.
对于一个恰有6列的方格表，由抽屉原理知至少有一列红点数不少于4，不妨设第1列，且第1列的前4行的小方格的中心是红点.如果某列有2个红点，则称其为某列上的一个红点“行对”.这样在前4行中，除第1列外的5列中每列只能有一个行对.于是，前4行中总共有
个行对.考虑最后两行：若第1列还有红点，那么，有红点的这一行不能再有其他的红点.如第1列还有2个红点，这时能增加9个行对，6×6方格表中共有11+9=20个行对；如第1 列还有1个红点，不妨设第1列第5行的小方格有红点，这时即使第6行除第1列外的其他小方格都有红点，那么，可增加
个行对，6×6方格表中共有11+14=25个行对；如第1列没有其他的红点，那么，在最后两行中最多还有两个行对，这两个行对占去了两列，在余下的三列中，每列最多有1个红点，于是，可增加行对2×5+3×2=16个，这时，6×6方格表中最多有11+16=27个行对.这说明27是可能的行对总数的最大值.
设第i列的红点数为
，
且
.则所有行对的总数
，即
.
由柯西不等式有
.
所以，
.
解得
.
由k为正整数知k≤21.这说明6×6方格表中红点个数最多为21个.
又当n≤5时，方格表中红点总数不大于4×5=20个.这说明n的最小值不小于7.
综上，该代表队至少有7名选手
