题目内容
顶点在同一球面上的正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=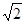 ,则
,则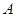 、
、 两点间的球面距离为
( )
两点间的球面距离为
( )
(A)  (B)
(B) 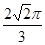 (C)
(C)  (D)
(D)
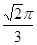
【答案】
A
【解析】正四棱柱的对角线为球的直径,由4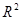 =1+1+2=4得R=1,设O为球心,在三角形OA
=1+1+2=4得R=1,设O为球心,在三角形OA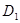 中,A
中,A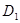 = 3 ,OA=O
= 3 ,OA=O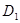 =1,所以∠AO
=1,所以∠AO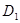 =
=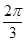 (其中O为球心),则A、
(其中O为球心),则A、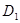 两点间的球面距离为
两点间的球面距离为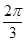 ,故选A.
,故选A.

练习册系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
顶点在同一球面上的正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=
,则A、D1两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
顶点在同一球面上的正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=
,则球的表面积为( )
| 2 |
| A、π | ||
B、
| ||
| C、4π | ||
| D、8π |