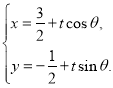题目内容
【题目】若定义在R上的偶函数![]() 满足
满足![]() ,且
,且![]() 时,
时,![]() ,则函数
,则函数![]() 的零点个数是( )
的零点个数是( )
A. 6个B. 8个C. 2个D. 4个
【答案】D
【解析】
先根据奇偶性和周期性作出f(x)在R上的图象,再在同一个坐标系中作出![]() 的图象,根据两图像交点个数即可得出h(x)的零点个数。
的图象,根据两图像交点个数即可得出h(x)的零点个数。
解:∵定义在R上的偶函数f(x)满足f(x+1)=﹣f(x),
∴满足f(x+2)=f(x),
故函数的周期为2.
当x∈[0,1]时,f(x)=x,
故当x∈[﹣1,0]时,f(x)=-x.
函数h(x)=f(x)﹣![]() 的零点的个数等于函数y=f(x)的图象与函数y=
的零点的个数等于函数y=f(x)的图象与函数y=![]() 的图象的交点个数.
的图象的交点个数.
在同一个坐标系中画出函数y=f(x)的图象与函数y=![]() 的图象,如图所示:
的图象,如图所示:
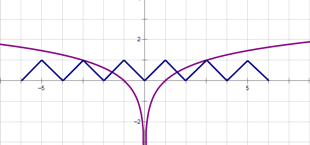
显然函数y=f(x)的图象与函数y=![]() 的图象有4个交点,
的图象有4个交点,
故选:D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目