题目内容
 如图,椭圆的中心在原点,其左焦点
如图,椭圆的中心在原点,其左焦点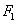 与抛物线
与抛物线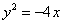 的焦点重合,过
的焦点重合,过 的直线
的直线 与椭圆交于A、B两点.当直线
与椭圆交于A、B两点.当直线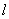 与x轴垂直时,
与x轴垂直时,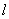 与抛物线交于C、D两点,
与抛物线交于C、D两点,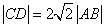 .
.
(Ⅰ)求椭圆的方程;
(II)求 的最大值和最小值.
的最大值和最小值.
【答案】
解:(Ⅰ)由抛物线方程,得焦点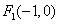 .
.
设椭圆的方程: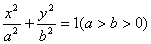 .
.
解方程组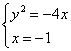 得C(-1,2),D(1,-2).
得C(-1,2),D(1,-2).
由于抛物线、椭圆都关于x轴对称,
∴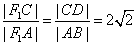 ,
,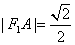 , ∴
, ∴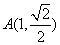 .
.
∴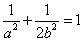 又
又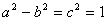 ,
,
因此,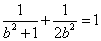 ,解得
,解得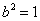 并推得
并推得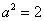 .
.
故椭圆的方程为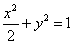 …………5分.
…………5分.
(Ⅱ)
由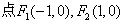
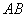 垂直于
垂直于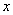 轴,则
轴,则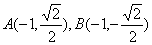 ,
,
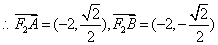 ,
,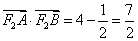
②若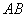 与
与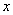 轴不垂直,设直线
轴不垂直,设直线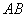 的斜率为
的斜率为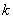 ,则直线
,则直线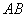 的方程为
的方程为
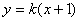
由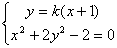 得
得 
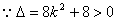 ,
, 方程有两个不等的实数根.
方程有两个不等的实数根.
设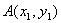 ,
,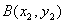 .
.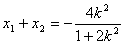 ,
, 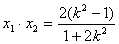
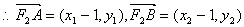
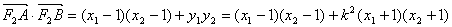
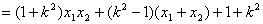
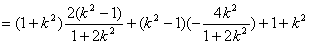
=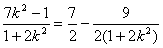
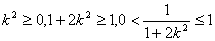
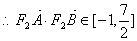 ,所以当直线
,所以当直线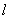 垂于
垂于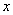 轴时,
轴时,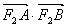 取得最大值
取得最大值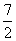 ;当直线
;当直线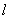 与
与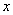 轴重合时,
轴重合时,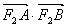 取得最小值
取得最小值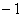 ………………12分
………………12分

练习册系列答案
相关题目
 如图,椭圆的中心在原点,F为椭圆的左焦点,B为椭圆的一个顶点,过点B作与FB垂直的直线BP交x轴于P点,且椭圆的长半轴长a和短半轴长b是关于x的方程
如图,椭圆的中心在原点,F为椭圆的左焦点,B为椭圆的一个顶点,过点B作与FB垂直的直线BP交x轴于P点,且椭圆的长半轴长a和短半轴长b是关于x的方程

 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上, 分别是椭圆
分别是椭圆 是椭圆短轴的一个端点,过
是椭圆短轴的一个端点,过 的直线
的直线 与椭圆交于
与椭圆交于 两点,
两点, 的面积为
的面积为 ,
, 的周长为
的周长为 .
. 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点 及以
及以 都相切,如存在,求出
都相切,如存在,求出
 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上, 分别是椭圆
分别是椭圆 是椭圆短轴的一个端点,过
是椭圆短轴的一个端点,过 的直线
的直线 与椭圆交于
与椭圆交于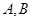 两点,
两点, 的面积为
的面积为 ,
, 的周长为
的周长为 .
.
 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点 及以
及以 都相切,如存在,求出
都相切,如存在,求出