题目内容
如图,椭圆的中心在原点,其左焦点![]() 与抛物线
与抛物线![]() 的焦点重合,过
的焦点重合,过![]() 的直线
的直线![]() 与椭圆交于A、B两点,与抛物线交于C、D两点.当直线
与椭圆交于A、B两点,与抛物线交于C、D两点.当直线![]() 与x轴垂直时,
与x轴垂直时,![]() .
.
(Ⅰ)求椭圆的方程;
(II)求过点O、![]() ,并且与椭圆的左准线相切的圆的方程;
,并且与椭圆的左准线相切的圆的方程;
(Ⅲ)求![]() 的最大值和最小值.
的最大值和最小值.

(Ⅰ)![]()
(Ⅱ)![]()
(Ⅲ)最大值![]() ,最小值
,最小值![]()
解析:
(Ⅰ)由抛物线方程,得焦点![]() .
.
设椭圆的方程:![]() .
.
解方程组 得C(-1,2),D(1,-2).
得C(-1,2),D(1,-2).
由于抛物线、椭圆都关于x轴对称,
∴![]() ,
,![]() , ∴
, ∴![]() . …………2分
. …………2分
∴![]() 又
又![]() ,
,
因此,![]() ,解得
,解得![]() 并推得
并推得![]() .
.
故椭圆的方程为![]() . …………4分
. …………4分
(Ⅱ)![]() ,
,
![]() 圆过点O、
圆过点O、![]() ,
,
![]() 圆心M在直线
圆心M在直线![]() 上.
上.
设![]() 则圆半径,由于圆与椭圆的左准线相切,
则圆半径,由于圆与椭圆的左准线相切,
∴![]()
由![]() 得
得![]() 解得
解得![]()
![]() 所求圆的方程为
所求圆的方程为![]() …………………………8分
…………………………8分
(Ⅲ) 由![]()
①若![]() 垂直于
垂直于![]() 轴,则
轴,则![]() ,
,
![]() ,
,
![]() …………………………………………9分
…………………………………………9分
②若![]() 与
与![]() 轴不垂直,设直线
轴不垂直,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为
![]()
由![]() 得
得 ![]()
![]() ,
,![]() 方程有两个不等的实数根.
方程有两个不等的实数根.
设![]() ,
,![]() .
.
![]() ,
, ![]() ………………………………11分
………………………………11分
![]()
![]()
![]()
![]()
=![]()
![]()
![]() ,所以当直线
,所以当直线![]() 垂于
垂于![]() 轴时,
轴时,![]() 取得最大值
取得最大值![]()
当直线![]() 与
与![]() 轴重合时,
轴重合时,![]() 取得最小值
取得最小值![]()

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 如图,椭圆的中心在原点,F为椭圆的左焦点,B为椭圆的一个顶点,过点B作与FB垂直的直线BP交x轴于P点,且椭圆的长半轴长a和短半轴长b是关于x的方程
如图,椭圆的中心在原点,F为椭圆的左焦点,B为椭圆的一个顶点,过点B作与FB垂直的直线BP交x轴于P点,且椭圆的长半轴长a和短半轴长b是关于x的方程
 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上, 分别是椭圆
分别是椭圆 是椭圆短轴的一个端点,过
是椭圆短轴的一个端点,过 的直线
的直线 与椭圆交于
与椭圆交于 两点,
两点, 的面积为
的面积为 ,
, 的周长为
的周长为 .
. 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点 及以
及以 都相切,如存在,求出
都相切,如存在,求出
 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上, 分别是椭圆
分别是椭圆 是椭圆短轴的一个端点,过
是椭圆短轴的一个端点,过 的直线
的直线 与椭圆交于
与椭圆交于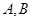 两点,
两点, 的面积为
的面积为 ,
, 的周长为
的周长为 .
.
 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点 及以
及以 都相切,如存在,求出
都相切,如存在,求出