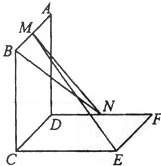
题目内容
如图,四边形PCBM是直角梯形, ,
, ∥
∥ ,
, .又
.又 ,
, ,直线AM与直线PC所成的角为
,直线AM与直线PC所成的角为 .
.
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
解析试题分析:方法1:(1)∵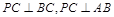 ,∴
,∴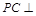 平面ABC,∴
平面ABC,∴ .5分
.5分
(2)取BC的中点N,连MN.∵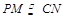 ,∴
,∴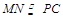 ,∴
,∴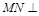 平面ABC.作
平面ABC.作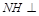
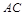 ,交AC的延长线于H,连结MH.由三垂线定理得
,交AC的延长线于H,连结MH.由三垂线定理得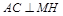 ,∴
,∴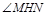 为二面角
为二面角 的平面角.∵直线AM与直线PC所成的角为
的平面角.∵直线AM与直线PC所成的角为 ,∴在
,∴在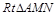 中,
中,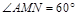 .
.
在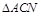 中,
中,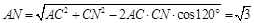 .
.
在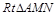 中,
中,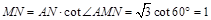 .
.
在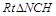 中,
中,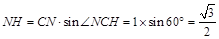 .
.
在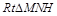 中,∵
中,∵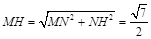 ,∴
,∴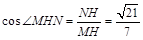 .
.
故二面角 的余弦值为
的余弦值为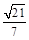 .13分
.13分
方法2:(1)∵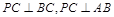 ,∴
,∴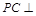 平面ABC,∴
平面ABC,∴ .5分
.5分
(2)在平面ABC内,过C作BC的垂线,并建立空间直角坐标系如图所示.设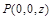 ,则
,则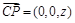 .
.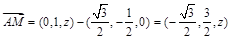 . 5分
. 5分
∵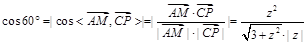 ,
,
且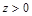 ,∴
,∴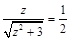 ,得
,得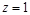 ,∴
,∴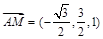 . 8分
. 8分
设平面MAC的一个法向量为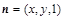 ,则由
,则由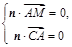 得
得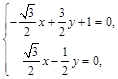 得
得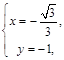 ∴
∴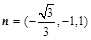 . 10分
. 10分
平面ABC的一个法向量为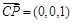 .
.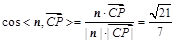 12分
12分
显然,二面角 为锐二面角,∴二面角
为锐二面角,∴二面角 的余弦值为
的余弦值为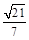 .13分
.13分
考点:二面角的平面角,线线垂直
点评:解决的关键是借助于空间向量法或几何性质法来得到证明和求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为圆
为圆 的直径,点
的直径,点 、
、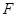 在圆
在圆 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 ,
,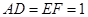 .
.
 平面
平面 ;
;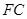 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;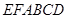 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为 ,
, ,求
,求 .
. ⊥平面
⊥平面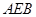 ,
, ,
, ,
, ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
 平面
平面 ;
; ;
;
 ,
,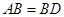 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.

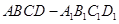 中,设
中,设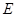 是棱
是棱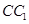 的中点.
的中点.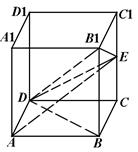
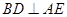 ;
;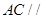 平面
平面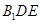 ;
;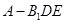 的体积.
的体积.
 是双曲线
是双曲线

 上一点,
上一点, 、
、 分别是双曲线
分别是双曲线 的左、右顶点,直线
的左、右顶点,直线 ,
,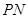 的斜率之积为
的斜率之积为 .
.
 ,
, 两点,
两点, 为坐标原点,
为坐标原点, 为双曲线上一点,满足
为双曲线上一点,满足 ,求
,求 的值.
的值.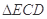 为等边三角形,F为ED边上的中点,且
为等边三角形,F为ED边上的中点,且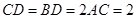 ,
,
 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.