题目内容
如图,在三棱柱ABC— 中,底面
中,底面 为正三角形,
为正三角形,
 平面ABC,
平面ABC, =2AB,N是
=2AB,N是 的中点,M是线段
的中点,M是线段 上的动点。
上的动点。
(1)当M在什么位置时, ,请给出证明;
,请给出证明;
(2)若直线MN与平面ABN所成角的大小为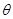 ,求
,求 的最大值。
的最大值。
(1)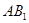 的中点;(2)
的中点;(2)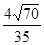
解析试题分析:(1)根据题意,由于在三棱柱ABC— 中,底面
中,底面 为正三角形,
为正三角形,
 平面ABC,
平面ABC, =2AB,N是
=2AB,N是 的中点,M是线段
的中点,M是线段 上的动点,根据题意猜想当点M在
上的动点,根据题意猜想当点M在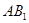 的中点时成立,证明:因为底面时正三角形侧面是矩形,高为2,底面边长设为1,那么可知根据线面垂直的性质定理能得到
的中点时成立,证明:因为底面时正三角形侧面是矩形,高为2,底面边长设为1,那么可知根据线面垂直的性质定理能得到
(2)根据线面角的定义,那么由于直线MN与平面ABN所成角的大小为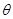 ,那么借助于平面ABN的垂线段来得到线面角,借助于长度的比列关系可知,
,那么借助于平面ABN的垂线段来得到线面角,借助于长度的比列关系可知, 的最大值
的最大值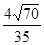 ,也可以通过建立空间直角坐标系来求解线面角,借助于向量法来得到三角函数关系式,进而求解最值。
,也可以通过建立空间直角坐标系来求解线面角,借助于向量法来得到三角函数关系式,进而求解最值。
考点:直线与平面之间的平行和垂直关系
点评:本题考查空间中直线与平面之间的平行和垂直关系,用空间向量求解夹角,本题解题的关键是建立坐标系,把理论的推导转化成数字的运算,降低了题目的难度

练习册系列答案
相关题目
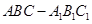 的所有棱长都为
的所有棱长都为 ,且
,且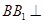 平面
平面 ,
, 为
为 中点.
中点.
 面
面 ;
; 的大小的余弦值;
的大小的余弦值; 到平面
到平面
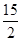 ,求AB的长.
,求AB的长.
 为圆
为圆 的直径,点
的直径,点 、
、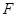 在圆
在圆 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 ,
,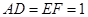 .
.
 平面
平面 ;
;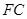 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;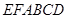 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为 ,
, ,求
,求 .
.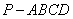 的底面
的底面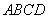 是等腰梯形,
是等腰梯形,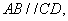 且
且

 分别是
分别是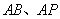 的中点.
的中点.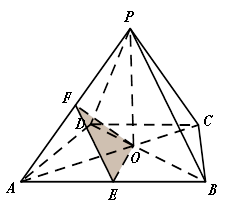
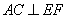 ;
;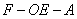 的余弦值.
的余弦值.  中,底面是边长为2的正方形,侧棱
中,底面是边长为2的正方形,侧棱 ,
, 为
为 的中点,
的中点, 是侧棱
是侧棱 上的一动点。
上的一动点。
 ;
; 时,求三棱锥
时,求三棱锥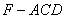 的体积.
的体积. 是正三角形,
是正三角形, 和
和 都垂直于平面
都垂直于平面 ,且
,且 ,
, 是
是 的中点.
的中点.
 平面
平面 .
. 
 是双曲线
是双曲线

 上一点,
上一点, 、
、 分别是双曲线
分别是双曲线 的左、右顶点,直线
的左、右顶点,直线 ,
,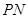 的斜率之积为
的斜率之积为 .
.
 ,
, 两点,
两点, 为坐标原点,
为坐标原点, 为双曲线上一点,满足
为双曲线上一点,满足 ,求
,求 的值.
的值.