题目内容
3.棱长为1的正方体ABCD-A1B1C1D1中,点M,N,P分别为AB1,BC1,DD1的中点,给出下列结论:①异面直线AB1,BC1所成的角为$\frac{π}{3}$
②MN∥平面ABCD
③四面体A-A1B1N的体积为$\frac{1}{4}$
④MN⊥BP
则正确结论的序号为①②④.
分析 根据正方体的性质,以及异面直线所成的角,得到异面直线AB1,BC1所成的角即为AD1与AB1所成的角,即可判断①,根据线面平行的判断定理即可判断②,根据正方体的体积为1,${S}_{△{A}_{1}{B}_{1}N}$=$\frac{1}{4}$${S}_{四边形{A}_{1}DC{B}_{1}}$,即可求出四面体A-A1B1N的体积,根据线面垂直得到线线垂直,即可判断④.
解答 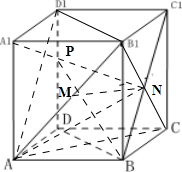 解:如图所示
解:如图所示
对于①连接AD1,B1D1,则BC1∥AD1,则异面直线AB1,BC1所成的角即为AD1与AB1所成的角,因为AD1=B1D1=AB1,所以异面直线AB1,BC1所成的角为$\frac{π}{3}$,故①正确;
对于②连接B1C,则交BC1与N,所以MN是三角形B1AC的中位线,所以MN∥AC,所以MN∥平面ABCD,故②正确;
对于③,连接A1D,AN,A1N,因为确;${S}_{△{A}_{1}{B}_{1}N}$=$\frac{1}{4}$${S}_{四边形{A}_{1}DC{B}_{1}}$,所以四面体A-A1B1N的体积为$\frac{1}{2}×\frac{1}{4}$×1=$\frac{1}{8}$;故③错误;
对于④,连接BO,因为AC⊥平面BB1D1D,所以MN⊥平面BB1D1D,又因为BP?平面BB1D1D,所以MN⊥BP
故④正确.
故答案为:①②④
点评 本题给出正方体模型,判断关于异面直线所成角的几个命题的真假性,着重考查了正方体的性质、异面直线所成角的求法等知识,属于中档题.

练习册系列答案
相关题目
18.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),M、N为双曲线上关于原点对称的两点,P为双曲线上的点,且直线PM、PN斜率分别为k1、k2,若k1•k2=$\frac{5}{4}$,则双曲线离心率为( )
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
15.某高三同学在七次月考考试中,数学成绩如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
| A. | 92,2 | B. | 92,2.8 | C. | 93,2 | D. | 93,2.8 |
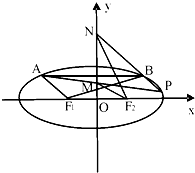 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4.
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4.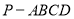 中,
中,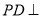 底面
底面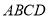 ,底面
,底面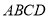 是直角梯形,
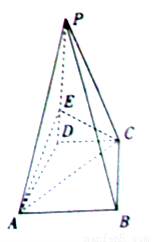
是直角梯形,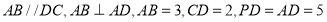 .
.
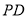 上确定一点
上确定一点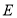 ,使得
,使得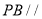 平面
平面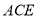 ,并求
,并求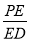 的值;
的值;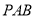 与平面
与平面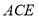 所成锐二面角的余弦值.
所成锐二面角的余弦值.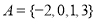 ,
,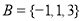 ,则
,则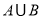 元素的个数为( )
元素的个数为( )