题目内容
已知函数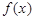 的定义域为
的定义域为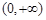 ,若
,若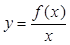 在
在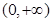 上为增函数,则称
上为增函数,则称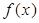 为“一阶比增函数”.
为“一阶比增函数”.
(Ⅰ) 若 是“一阶比增函数”,求实数
是“一阶比增函数”,求实数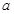 的取值范围;
的取值范围;
(Ⅱ) 若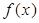 是“一阶比增函数”,求证:
是“一阶比增函数”,求证: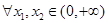 ,
,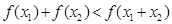 ;
;
(Ⅲ)若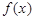 是“一阶比增函数”,且
是“一阶比增函数”,且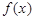 有零点,求证:
有零点,求证: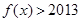 有解.
有解.
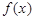 的定义域为
的定义域为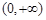 ,若
,若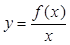 在
在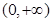 上为增函数,则称
上为增函数,则称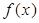 为“一阶比增函数”.
为“一阶比增函数”.(Ⅰ) 若
 是“一阶比增函数”,求实数
是“一阶比增函数”,求实数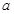 的取值范围;
的取值范围;(Ⅱ) 若
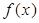 是“一阶比增函数”,求证:
是“一阶比增函数”,求证: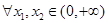 ,
,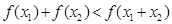 ;
;(Ⅲ)若
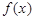 是“一阶比增函数”,且
是“一阶比增函数”,且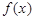 有零点,求证:
有零点,求证: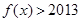 有解.
有解. (Ⅰ) 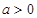 (Ⅱ)本小题关键是先得到
(Ⅱ)本小题关键是先得到 ,
, 
(Ⅲ)本小题要结合(Ⅱ)的结论来证明。
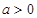 (Ⅱ)本小题关键是先得到
(Ⅱ)本小题关键是先得到 ,
, 
(Ⅲ)本小题要结合(Ⅱ)的结论来证明。
试题分析:解:(I)由题
 在
在 是增函数,
是增函数,由一次函数性质知
当
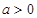 时,
时, 在
在 上是增函数,
上是增函数,所以
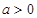
(Ⅱ)因为
 是“一阶比增函数”,即
是“一阶比增函数”,即 在
在 上是增函数,
上是增函数,又
 ,有
,有 ,
,
所以
 ,
, 
所以
 ,
,
所以

所以

(Ⅲ)设
 ,其中
,其中 .
.因为
 是“一阶比增函数”,所以当
是“一阶比增函数”,所以当 时,
时,
取
 ,满足
,满足 ,记
,记
由(Ⅱ)知
 ,同理
,同理 ,
,
所以一定存在
 ,使得
,使得 ,
,所以
 一定有解
一定有解 点评:证明函数
 在区间
在区间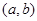 上为增(减)函数的方法是:令
上为增(减)函数的方法是:令 ,若
,若
(
 ),则函数为增(减)函数。
),则函数为增(减)函数。
练习册系列答案
相关题目
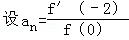 ,则a100= .
,则a100= .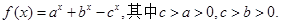
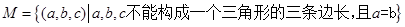 ,则
,则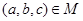 所对应的
所对应的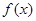 的零点的取值集合为____。
的零点的取值集合为____。 .(写出所有正确结论的序号)
.(写出所有正确结论的序号)
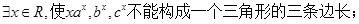
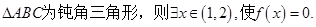
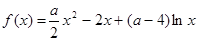 ,
,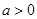 .
.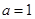 ,求函数
,求函数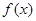 的极值;
的极值;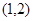 上有极值,求
上有极值,求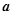 的取值范围.
的取值范围.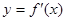 的图象如图所示,则
的图象如图所示,则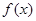 的解析式可能是 ( )
的解析式可能是 ( ) 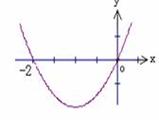
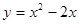
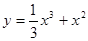
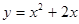
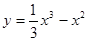
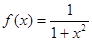
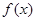 的奇偶性;
的奇偶性;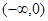 上是增函数还是减函数?证明你的结论.
上是增函数还是减函数?证明你的结论.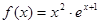 ,
,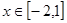 的最大值为
的最大值为