题目内容
若存在实数k,b,使得函数f(x)和g(x)对其定义域上的任意实数x同时满足:f(x)≥kx+b且g(x)≤kx+b,则称直线:l:y=kx+b为函数f(x)和g(x)的“隔离直线”.已知f(x)=x2,g(x)=2elnx(其中e为自然对数的底数).试问:
(1)函数f(x)和g(x)的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
(2)函数f(x)和g(x)是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
(1)函数f(x)和g(x)的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
(2)函数f(x)和g(x)是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
分析:(1)根据求导公式,求出函数的导数,根据导数判断函数的单调性并求极值,从而可知,函数f(x)和g(x)的图象在x=
处有公共点
(2)存在f(x)和g(x)的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k.则隔离直线方程为y-e=k(x-
,即y=kx-k
+e,构造函数,求出函数函数的导数,根据导数求出函数的最值
| e |
(2)存在f(x)和g(x)的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k.则隔离直线方程为y-e=k(x-
| e |
| e |
解答:解:(1)∵F(x)=f(x)-g(x)=x2-2elnx(x>0),
∴F′(x)=2x-
=
令F′(X)=0,得x=
,
当0<x<
时,F′(X)<0,X>
时,F′(x)>0
故当x=
时,F(x)取到最小值,最小值是0
从而函数f(x)和g(x)的图象在x=
处有公共点
(2)由(1)可知,函数f(x)和g(x)的图象在x=
处有公共点,因此存在f(x)和g(x)的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k.则隔离直线方程为y-e=k(x-
,即y=kx-k
+e
由f(x)≥kx-k
+e(x?R),可得x2-kx-k
+e,
由f(x)≥kx-k
+e(x?R),可得x2-kx+k
-e≥0当x?R恒成立,
则△=k2-4k
+4e=(k-2
)2≤0,只有k=2
,此时直线方程为:y=2
x-e,
下面证明g(x)≤2
x-eexx>0恒成立,
令G(x)=2
x-e-g(x)=2
x-e-2elnx,
G′(X)=2
-
=(2
x-2c)/x=2
(x-
)/x,
当x=
时,G′(X)=0,当0<x<
时G′(X)>0,
则当x=
时,G(x)取到最小值,极小值是0,也是最小值.
所以G(x)=2
x-e-g(x)≥0,则g(x)≤2
x-e当x>0时恒成立.
∴函数f(x)和g(x)存在唯一的隔离直线y=2
x-e
∴F′(x)=2x-
| 2e |
| x |
2(x-
| ||||
| x |
令F′(X)=0,得x=
| e |
当0<x<
| e |
| e |
故当x=
| e |
从而函数f(x)和g(x)的图象在x=
| e |
(2)由(1)可知,函数f(x)和g(x)的图象在x=
| e |
| e |
| e |
由f(x)≥kx-k
| e |
| e |
由f(x)≥kx-k
| e |
| e |
则△=k2-4k
| e |
| c |
| e |
| e |
下面证明g(x)≤2
| e |
令G(x)=2
| e |
| e |
G′(X)=2
| c |
| 2c |
| x |
| c |
| c |
| e |
当x=
| e |
| e |
则当x=
| e |
所以G(x)=2
| e |
| e |
∴函数f(x)和g(x)存在唯一的隔离直线y=2
| e |
点评:本题以函数为载体,考查新定义,关键是对新定义的理解,考查函数的求导,利用导数求最值,属于难题.

练习册系列答案
相关题目
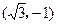 ,b=
,b=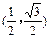
 b;
b; b,y=-ka+tb,且x
b,y=-ka+tb,且x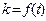 ;
;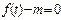 的解的情况。
的解的情况。 ,b=
,b=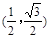
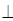 b;
b; b,y=-ka+tb,且x
b,y=-ka+tb,且x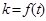 ;
;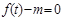 的解的情况。
的解的情况。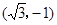 ,b=
,b=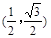
 b;
b;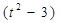 b,y=-ka+tb,且x
b,y=-ka+tb,且x ;
; 的解的情况。
的解的情况。