题目内容
【题目】随着科技的发展,网购已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在某市的普及情况,某调查机构进行了有关网购的调查,并从参与调查的市民中随机抽取了男、女各100人进行分析,得到如下所示的统计表.
经常网购 | 偶尔网购或不网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
附: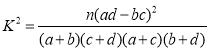 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为该市市民的网购情况与性别无关.
(2)①现从所抽取的100位女性市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从该市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为X,求随机变量X的数学期望和方差.
【答案】(1)见解析,能(2)①![]() ②数学期望6,方差2.4.
②数学期望6,方差2.4.
【解析】
(1)完善列联表,计算![]() ,得到答案.
,得到答案.
(2)计算得到![]() ,根据题意知
,根据题意知![]() ,计算数学期望和方差得到答案.
,计算数学期望和方差得到答案.
(1)完成列联表如下图所示.
经常网购 | 偶尔网购或不网购 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 70 | 30 | 100 |
合计 | 120 | 80 | 200 |
由列联表,得![]() ,
,
∴能在犯错误的概率不超过0.01的前提下认为该市市民的网购情况与性别有关.
(2)①由题意知所抽取的10位女性市民中,经常网购的有![]() (人),
(人),
偶尔网购或不网购的有![]() (人),
(人),
∴选取的3人中至少有2人经常网购的概率![]() .
.
②由![]() 列联表可知,抽到经常网购的市民的频率为
列联表可知,抽到经常网购的市民的频率为![]() ,将频率视为概率,
,将频率视为概率,
∴从该市所有参与调查的市民中任意抽取一人,抽到经常网购的市民的概率为0.6,
∴由题意知![]() .
.
∴随机变量X的数学期望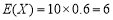 ,方差
,方差![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某班主任对全班50名学生学习积极性和对待工作的态度进行了调查,统计数据如下所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法有多大把握认为学生的学习积极性与对班级工作的态度有关系?并说明理由.
本题参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |