题目内容
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 外的点
外的点![]() 在
在![]() 轴的右侧运动,且
轴的右侧运动,且![]() 到圆
到圆![]() 上的点的最小距离等于它到
上的点的最小距离等于它到![]() 轴的距离,记
轴的距离,记![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的直线交
的直线交![]() 于
于![]() ,
,![]() 两点,以
两点,以![]() 为直径的圆
为直径的圆![]() 与平行于
与平行于![]() 轴的直线相切于点
轴的直线相切于点![]() ,线段
,线段![]() 交
交![]() 于点
于点![]() ,证明:
,证明:![]() 的面积是
的面积是![]() 的面积的四倍.
的面积的四倍.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
法一:(1)设P(x,y),x>0,F(1,0).由点P在⊙F外,可得点P到⊙F上的点的最小距离为|PF|﹣1,由题意可得:|PF|﹣1=x,利用两点之间的距离公式即可得出.
(2)设N(x0,y0),A(x1,y1),B(x2,y2).则D(![]() ,
,![]() ).由题意可设直线AB的方程为:y=k(x﹣1)(k≠0).与抛物线方程联立化为:k2x2﹣(2k2+4)x+k2=0.利用根与系数的关系、中点坐标公式可得D,M,N的坐标.再利用三角形面积计算公式即可得出.
).由题意可设直线AB的方程为:y=k(x﹣1)(k≠0).与抛物线方程联立化为:k2x2﹣(2k2+4)x+k2=0.利用根与系数的关系、中点坐标公式可得D,M,N的坐标.再利用三角形面积计算公式即可得出.
法二:(1)由题意得,点![]() 到圆
到圆![]() 的距离
的距离![]() 等于
等于![]() 到直线
到直线![]() 的距离,根据抛物线的定义求得轨迹方程. (2)设
的距离,根据抛物线的定义求得轨迹方程. (2)设![]() ,
,![]() ,由题意可设直线AB的方程为:
,由题意可设直线AB的方程为:![]() 与抛物线方程联立,利用根与系数的关系、中点坐标公式可得D的坐标,结合
与抛物线方程联立,利用根与系数的关系、中点坐标公式可得D的坐标,结合
![]() ,可得
,可得![]() ,进而求出N的坐标,利用点的位置关系得到面积的关系.
,进而求出N的坐标,利用点的位置关系得到面积的关系.
法三:(1)与法一同;(2)设![]() ,
,![]() ,由题意可设直线AB的方程为:
,由题意可设直线AB的方程为:![]() 与抛物线方程联立,利用根与系数的关系、中点坐标公式可得D,M的坐标,利用斜率公式计算得到
与抛物线方程联立,利用根与系数的关系、中点坐标公式可得D,M的坐标,利用斜率公式计算得到![]() ,再利用长度关系得到面积的关系.
,再利用长度关系得到面积的关系.
解法一:(1)设![]() ,依题意
,依题意![]() ,
,![]() .
.
因为![]() 在圆
在圆![]() 外,所以
外,所以![]() 到圆
到圆![]() 上的点的最小距离为
上的点的最小距离为![]()
依题意得![]() ,即
,即![]() ,
,
化简得![]() 的方程为
的方程为![]() .
.
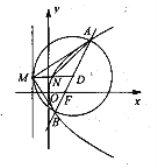
(2)设![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
依题意可设直线![]() 的方程
的方程![]() ,
,
由![]() 得
得![]() .
.
因为![]() ,
,
所以![]() ,
,
则有![]() ,故
,故![]() ,
,
由抛物线的定义知![]() .
.
设![]() ,依题意得
,依题意得![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() ,
,
解得![]() ,所以
,所以![]() .,
.,
因为![]() 在抛物线上,所以
在抛物线上,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
![]() ,
,
故![]()
解法二:(1)设![]() ,依题意
,依题意![]() .
.
因为![]() 在圆
在圆![]() 外,所以
外,所以![]() 到圆
到圆![]() 上的点的最小距离为
上的点的最小距离为![]() .
.
依题意得,点![]() 到圆
到圆![]() 的距离
的距离![]() 等于
等于![]() 到直线
到直线![]() 的距离,
的距离,
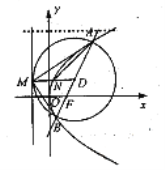
所以![]() 在以
在以![]() 为焦点,
为焦点,![]() 为准线的抛物线上.
为准线的抛物线上.
所以![]() 的方程为
的方程为![]() ..
..
(2)设![]() ,
,![]() ,
,
因为直线![]() 过
过![]() ,依题意可设其方程
,依题意可设其方程![]()
由![]() 得
得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
则有![]() .
.
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
由抛物线的定义得![]() .,
.,
设圆![]() 与
与![]() 相切于
相切于![]() ,
,
因为![]() 与抛物线相交于
与抛物线相交于![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
设![]() ,则
,则![]() ,且
,且![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又因为![]() 为
为![]() 的中点,
的中点,![]() ,所以
,所以![]() .
.
解法三:(1)同解法一.
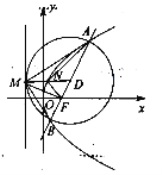
(2)设![]() ,
,![]() ,连结
,连结![]() ,
,![]() .
.
因为直线![]() 过
过![]() ,依题意可设其方程
,依题意可设其方程![]()
由![]() 得
得![]() .,
.,
因为![]() ,所以
,所以![]() ,
,
所以![]() .
.
因为![]() ,
,![]() ,又因为
,又因为![]() ,
,
所以![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
所以![]() ,故
,故![]() .
.
又因为![]() ,所以
,所以![]() ,从而
,从而![]() .
.
所以![]() ,
,
又![]() ,所以
,所以![]() .
.

【题目】为降低汽车尾气排放量,某工厂设计制造了![]() 、
、![]() 两种不同型号的节排器,规定性能质量评分在
两种不同型号的节排器,规定性能质量评分在![]() 的为优质品.现从该厂生产的
的为优质品.现从该厂生产的![]() 、
、![]() 两种型号的节排器中,分别随机抽取500件产品进行性能质量评分,并将评分分别分成以下六个组;
两种型号的节排器中,分别随机抽取500件产品进行性能质量评分,并将评分分别分成以下六个组;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制成如图所示的频率分布直方图:
,绘制成如图所示的频率分布直方图:
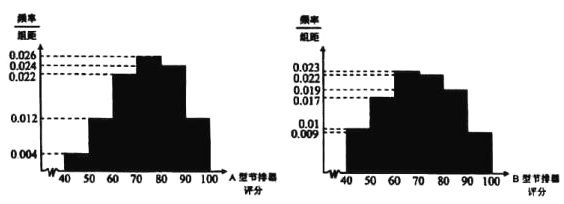
(1)设500件![]() 型产品性能质量评分的中位数为
型产品性能质量评分的中位数为![]() ,直接写出
,直接写出![]() 所在的分组区间;
所在的分组区间;
(2)请完成下面的列联表(单位:件)(把有关结果直接填入下面的表格中);
|
| 总计 | |
优质品 | |||
非优质品 | |||
总计 | 500 | 500 | 1000 |
(3)根据(2)中的列联表,能否有![]() 的把握认为
的把握认为![]() 、
、![]() 两种不同型号的节排器性能质量有差异?
两种不同型号的节排器性能质量有差异?
附:![]() ,其中
,其中![]() .
.
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100~110的学生数有21人。

(Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占![]() )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;
(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩。
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据![]() 其回归线
其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.