题目内容
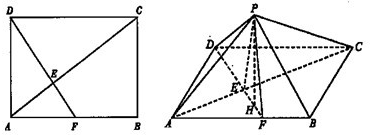
如图,矩形ABCD中,AB=a,AD=b,过点D作DE⊥AC于E,交直线AB于F.现将△ACD沿对角线AC折起到△PAC的位置,使二面角P-AC-B的大小为60°.过P作PH⊥EF于H.
(I)求证:PH⊥平面ABC;
(Ⅱ)若a=
b,求直线DP与平面PBC所成角的大小;
(Ⅲ)若a+b=2,求四面体P-ABC体积的最大值.
(I)求证:PH⊥平面ABC;
(Ⅱ)若a=
| 2 |
(Ⅲ)若a+b=2,求四面体P-ABC体积的最大值.

分析:(I)证明AC⊥平面PEF,可得平面PEF⊥平面ABC,利用面面垂直的性质,可得PH⊥平面ABC;
(II)以D为原点,DA,DC所在直线分别为x,y轴,DA的长度为单位长度,建立空间直角坐标系,求出平面PBC的法向量,利用向量的夹角公式,即可求直线DP与平面PBC所成角的大小;
(Ⅲ)表示出四面体P-ABC体积,根据a+b=2,利用基本不等式,即可求四面体P-ABC体积的最大值.
(II)以D为原点,DA,DC所在直线分别为x,y轴,DA的长度为单位长度,建立空间直角坐标系,求出平面PBC的法向量,利用向量的夹角公式,即可求直线DP与平面PBC所成角的大小;
(Ⅲ)表示出四面体P-ABC体积,根据a+b=2,利用基本不等式,即可求四面体P-ABC体积的最大值.
解答: (I)证明:∵AC⊥PE,AC⊥EF,又PE∩EF=E,∴AC⊥平面PEF,
(I)证明:∵AC⊥PE,AC⊥EF,又PE∩EF=E,∴AC⊥平面PEF,
∵AC?平面ABC,∴平面PEF⊥平面ABC,
∵平面PEF∩平面ABC=EF,PH⊥EF,PH?平面PEF,
∴PH⊥平面ABC.
(II)解:∵PE⊥AC,EF⊥AC
∴∠PEF为二面角P-AC-B的平面角,∴∠PEF=60°
∴EH=
PE=
DE,PH=
DE,DH=
DE
以D为原点,DA,DC所在直线分别为x,y轴,DA的长度为单位长度,建立空间直角坐标系,则DC=
,A(1,0,0),B(1,
,0),C(0,
,0)
∴AC=
,DE=
=
,
∴DH=
DE=
,PH=
DE=
作HM⊥AD于M,HN⊥CD于N
∵∠ADF=∠DCA
∴HM=DHsin∠ADF=DHsin∠DCF=
,DM=
=1
∴H(1,
,0),P(1,
,
)
∴
=(0,-
,
),
=(1,-
,
)
设平面PBC的法向量为
=(x,y,z),则由
,可得
∴可取
=(0,1,1)
设直线DP与平面PBC所成角的大小为θ,则sinθ=|
|=
∴θ=45°
∴直线DP与平面PBC所成角的大小为45°;
(III)PE=DE=
,∴PH=
DE=
∴VP-ABC=
•
AB•BC•PH=
•
∵a+b=2
∴a2+b2=(a+b)2-2ab=4-2ab
由ab≤(
)2=1,当且仅当a=b=1时,(ab)max=1
∴V=
•
=
•
=
•
≤
•
=
即当且仅当a=b=1时,四面体P-ABC体积的最大值为
.
 (I)证明:∵AC⊥PE,AC⊥EF,又PE∩EF=E,∴AC⊥平面PEF,
(I)证明:∵AC⊥PE,AC⊥EF,又PE∩EF=E,∴AC⊥平面PEF,∵AC?平面ABC,∴平面PEF⊥平面ABC,
∵平面PEF∩平面ABC=EF,PH⊥EF,PH?平面PEF,
∴PH⊥平面ABC.
(II)解:∵PE⊥AC,EF⊥AC
∴∠PEF为二面角P-AC-B的平面角,∴∠PEF=60°
∴EH=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
以D为原点,DA,DC所在直线分别为x,y轴,DA的长度为单位长度,建立空间直角坐标系,则DC=
| 2 |
| 2 |
| 2 |
∴AC=
| 3 |
| DA•DC |
| AC |
| ||
| 3 |
∴DH=
| 3 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
作HM⊥AD于M,HN⊥CD于N
∵∠ADF=∠DCA
∴HM=DHsin∠ADF=DHsin∠DCF=
| ||
| 2 |
| DH2-HM2 |
∴H(1,
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| BP |
| ||
| 2 |
| ||
| 2 |
| CP |
| ||
| 2 |
| ||
| 2 |
设平面PBC的法向量为
| n |
|
|
∴可取
| n |
设直线DP与平面PBC所成角的大小为θ,则sinθ=|
| ||||
|
|
| ||
| 2 |
∴θ=45°
∴直线DP与平面PBC所成角的大小为45°;
(III)PE=DE=
| ab | ||
|
| ||
| 2 |
| ||
2
|
∴VP-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 12 |
| a2b2 | ||
|
∵a+b=2
∴a2+b2=(a+b)2-2ab=4-2ab
由ab≤(
| a+b |
| 2 |
∴V=
| ||
| 12 |
| a2b2 | ||
|
| ||
| 12 |
| a2b2 | ||
|
| ||
| 12 |
| a2b2 | ||
|
| ||
| 12 |
| 1 | ||
|
| ||
| 24 |
即当且仅当a=b=1时,四面体P-ABC体积的最大值为
| ||
| 24 |
点评:本题考查线面垂直,面面垂直,考查线面角,考查四面体体积的计算,考查学生分析解决问题的能力,难度大.

练习册系列答案
相关题目
 如图,矩形ABCD中,AB=
如图,矩形ABCD中,AB=
 A 若方程ax-x-a=0有两个实数解,则a的取值范围是
A 若方程ax-x-a=0有两个实数解,则a的取值范围是 如图,矩形ABCD中,
如图,矩形ABCD中, (理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD