题目内容
已知函数
（a≥0）．
（1）当a=1时，判断函数f（x）在其定义域内是否存在极值？若存在，求出极值，若不存在，说明理由；
（2）若函数f（x）在其定义域内为单调函数，求a的取值范围．
解：（1）∵
（x＞0），
∴
，
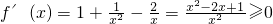∴f（x）在（0，+∞）单调递增，
∴f（x）无极值．
（2）
，
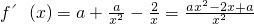①a=0时，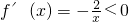
，
∴f（x）在（0，+∞）单调递减；
②a＞0时，f（x）在（0，+∞）上只可能单调递增，
∴f'（x）≥0在（0，+∞）上恒成立，
即ax2-2x+a≥0在（0，+∞）上恒成立，
即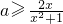
在（0，+∞）上恒成立，
∵
，
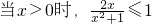∴a≥1．
综合上述a的取值范围是[1，+∞）∪{0}．
分析：（1）由（x＞0），知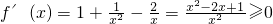，由此能判断f（x）在在其定义域内是否存在极值．
（2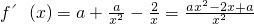），由此根据a的取值范围进行分类讨论，能够求出a的取值范围．
点评：本题考查函数的极值是否存在，考查函数的单调性的灵活运用，解题时要认真审题，仔细解答，注意导数性质的合理运用．
（x＞0），∴
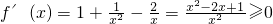，∴f（x）在（0，+∞）单调递增，
∴f（x）无极值．
（2）
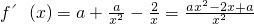，①a=0时，
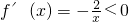，∴f（x）在（0，+∞）单调递减；
②a＞0时，f（x）在（0，+∞）上只可能单调递增，
∴f'（x）≥0在（0，+∞）上恒成立，
即ax2-2x+a≥0在（0，+∞）上恒成立，
即
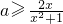在（0，+∞）上恒成立，∵
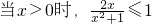，∴a≥1．
综合上述a的取值范围是[1，+∞）∪{0}．
分析：（1）由
（x＞0），知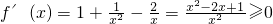，由此能判断f（x）在在其定义域内是否存在极值．（2）
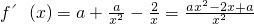，由此根据a的取值范围进行分类讨论，能够求出a的取值范围．点评：本题考查函数的极值是否存在，考查函数的单调性的灵活运用，解题时要认真审题，仔细解答，注意导数性质的合理运用．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
（a≠0且a≠1）．
上单调递减，在
上单调递增，求a的值并写出函数的解析式；
（a≠0且a≠1）．
上单调递减，在
上单调递增，求a的值并写出函数
的解析式；
的图象为曲线C，试问是否存在经过原点的直线l，使得l为曲线C的对称轴？若存在，求出l的方程；若不存在，请说明理由．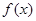
，若存在x0∈R，使方程
成立，则称x0为
（a≠0）．
时，求函数
，若存在x0∈R，使
成立，则称x0为
（a≠0）。
时，求函数
图象上A、B两点的横坐标是函数
对称，求
的的最小值。
已知函数 
若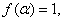
=