题目内容
(本小题满10分)注意:第(3)小题平行班学生不必做,特保班学生必须做。对于函数 ,若存在x0∈R,使
,若存在x0∈R,使 成立,则称x0为
成立,则称x0为 的不动点。已知函数
的不动点。已知函数 (a≠0)。
(a≠0)。
(1)当 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意实数b,函数 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
(3)(特保班做) 在(2)的条件下,若 图象上A、B两点的横坐标是函数
图象上A、B两点的横坐标是函数 的不动点,且A、B两点关于点
的不动点,且A、B两点关于点 对称,求
对称,求 的的最小值。
的的最小值。
【答案】
(1)3和-1;
(2)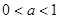
(3)b的最小值为-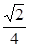 。
。
【解析】(1)由题得: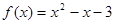 ,因为
,因为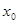 为不动点,
为不动点,
因此有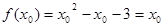 ,即
,即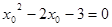
所以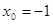 或
或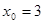 ,即3和-1为
,即3和-1为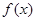 的不动点。
的不动点。
(2)因为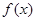 恒有两个不动点,
恒有两个不动点,
∴ 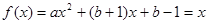 ,
,
即 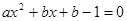 (※)恒有两个不等实数根,
(※)恒有两个不等实数根,
由题设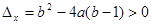 恒成立,
恒成立,
即对于任意b∈R,有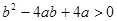 恒成立,
恒成立,
所以有 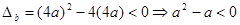 ,
,
∴ 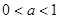 。
。
(3)由(※)式得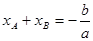 ,由题得E是A、B的中点,且
,由题得E是A、B的中点,且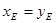
∴ 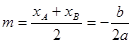 ,则E(
,则E( ),
),
∴ - , ∴ b=-
, ∴ b=-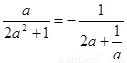 ,
,
又由(2)知 0<a<1, 令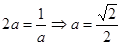
∴ 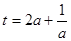 在
在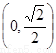 上是单调递减,在
上是单调递减,在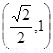 上是单调递增
上是单调递增
∴ 当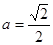 时,
时,
即 当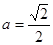 时, b取得最小值,其最小值为-
时, b取得最小值,其最小值为-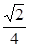 。
。

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
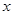 小时,但他须交纳个人住房公积金和失业保险(这两项费用为每周总收入的10%).试分析算法步骤并画出其每周净得工资
小时,但他须交纳个人住房公积金和失业保险(这两项费用为每周总收入的10%).试分析算法步骤并画出其每周净得工资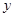 元的算法的程序框图.(注:满工作量外的工作时间为加班)
元的算法的程序框图.(注:满工作量外的工作时间为加班)