题目内容
已知函数 (a≠0且a≠1).
(a≠0且a≠1).(Ⅰ)试就实数a的不同取值,写出该函数的单调递增区间;
(Ⅱ)已知当x>0时,函数在
 上单调递减,在
上单调递减,在 上单调递增,求a的值并写出函数
上单调递增,求a的值并写出函数 的解析式;
的解析式;(Ⅲ)记(Ⅱ)中的函数
 的图象为曲线C,试问是否存在经过原点的直线l,使得l为曲线C的对称轴?若存在,求出l的方程;若不存在,请说明理由.
的图象为曲线C,试问是否存在经过原点的直线l,使得l为曲线C的对称轴?若存在,求出l的方程;若不存在,请说明理由.
【答案】分析:(1)对函数f(x)进行求导,令导函数大于0根据a的不同值求出x的范围.
(2)令f'( )=0求出a即可得到答案.
)=0求出a即可得到答案.
(3)假设存在且设直线方程y=kx,根据点的对称求出直线斜率即可得到答案.
解答:解:(Ⅰ)由题设知: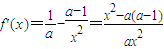 .
.
①当a<0时,函数f(x)的单调递增区间为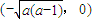
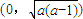 ;
;
②当0<a<1时,函数f(x)的单调递增区间为(-∞,0)及(0,+∞);
③当a>1时,函数f(x)的单调递增区间为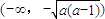 及
及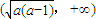 .
.
(Ⅱ)由题设及(Ⅰ)中③知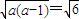 且a>1,解得a=3,
且a>1,解得a=3,
因此,函数解析式为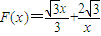 (x≠0).
(x≠0).
(Ⅲ)假设存在经过原点的直线l为曲线C的对称轴,显然x、y轴不是曲线C的对称轴,
故可设l:y=kx(k≠0),设P(p,q)为曲线C上的任意一点,P'(p',q')与P(p,q)关于直线l对称,且p≠p',q≠q',
则P'也在曲线C上,由此得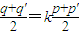 ,
,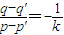 ,且
,且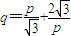 ,
,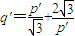 ,
,
整理得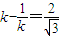 ,解得
,解得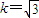 或
或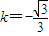 ,
,
所以存在直线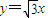 及
及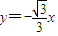 为曲线C的对称轴.
为曲线C的对称轴.
点评:本题主要考查函数的单调性与其导函数的正负的关系,即导函数大于0时原函数单调递增,导函数小于0时原函数单调递减.
(2)令f'(
 )=0求出a即可得到答案.
)=0求出a即可得到答案.(3)假设存在且设直线方程y=kx,根据点的对称求出直线斜率即可得到答案.
解答:解:(Ⅰ)由题设知:
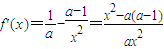 .
.①当a<0时,函数f(x)的单调递增区间为
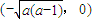
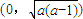 ;
;②当0<a<1时,函数f(x)的单调递增区间为(-∞,0)及(0,+∞);
③当a>1时,函数f(x)的单调递增区间为
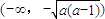 及
及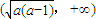 .
.(Ⅱ)由题设及(Ⅰ)中③知
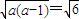 且a>1,解得a=3,
且a>1,解得a=3,因此,函数解析式为
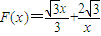 (x≠0).
(x≠0).(Ⅲ)假设存在经过原点的直线l为曲线C的对称轴,显然x、y轴不是曲线C的对称轴,
故可设l:y=kx(k≠0),设P(p,q)为曲线C上的任意一点,P'(p',q')与P(p,q)关于直线l对称,且p≠p',q≠q',
则P'也在曲线C上,由此得
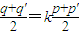 ,
,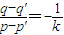 ,且
,且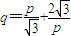 ,
,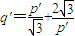 ,
,整理得
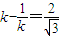 ,解得
,解得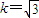 或
或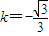 ,
,所以存在直线
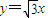 及
及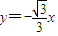 为曲线C的对称轴.
为曲线C的对称轴.点评:本题主要考查函数的单调性与其导函数的正负的关系,即导函数大于0时原函数单调递增,导函数小于0时原函数单调递减.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 (a≠0且a≠1).
(a≠0且a≠1). 上单调递减,在
上单调递减,在 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;