题目内容
(本题满分12分)在 中,角
中,角 所对的边为
所对的边为 已知
已知 .
.
(1)求 值;(2)若
值;(2)若 面积为
面积为 ,且
,且 ,求
,求 值.
值.
(Ⅰ)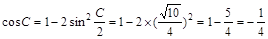 ;(Ⅱ)
;(Ⅱ)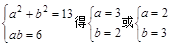 。
。
解析试题分析: (1)根据二倍角公式来得到角C的余弦值。
(2)在第二问中,结合三角形的面积公式,以及正弦定理,化角为边,然后得到边的关系,结合角C的余弦定理得到ab的值,进而解得。
解:(Ⅰ)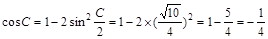 ……………………4分
……………………4分
(Ⅱ)∵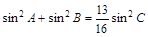 ,由正弦定理可得:
,由正弦定理可得: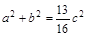
由(Ⅰ)可知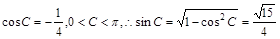 .
.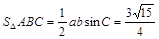 ,
,
得ab=6………………………………………………8分
由余弦定理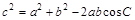
可得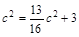
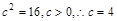 …………………………………………10分
…………………………………………10分
由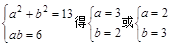 ……………12分
……………12分
考点:本题主要考查解三角形中正弦定理和余弦定理的运用,以及三角形的面积公式的综合运用问题。
点评:解决该试题的关键是就已知中关系式利用二倍角公式化简得到交C的余弦值,进而结合正弦定理得到a,b,c的平方关系,和余弦定理得到a,b的值。

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
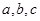 分别为
分别为 三个内角
三个内角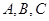 的对边,且
的对边,且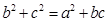 .
.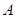 的大小;
的大小;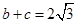 ,
,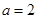 ,求
,求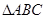 的面积.
的面积.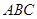 的内角
的内角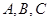 所对的边分别为
所对的边分别为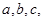 且
且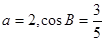 .
.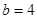 , 求
, 求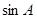 的值;
的值;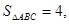 求
求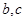 的值.
的值. 海里,则灯塔和轮船原来的距离为多少?
海里,则灯塔和轮船原来的距离为多少?
 的内角
的内角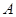 、
、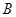 、
、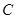 的对边分别为
的对边分别为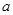 、
、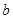 、
、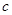 ,已知
,已知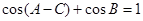 ,
,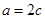 ,求
,求 。
。 的值;
的值; ,求
,求 和
和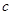 。
。 ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=
ABC中,内角A,B,C的对边分别为a,b,c.已知cosA= ,sinB=
,sinB= cosC.
cosC. ,求
,求 中,内角
中,内角 对边的边长分别是
对边的边长分别是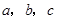 ,已知
,已知 ,
, ,
, ,求
,求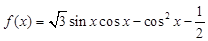 ,
,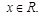
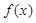 的最大值和最小正周期;
的最大值和最小正周期;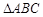 的内角
的内角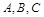 的对边分别
的对边分别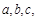 且
且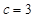 ,
,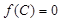 ,若
,若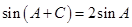 ,求
,求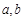 的值.
的值.