题目内容
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
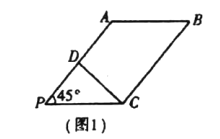
是![]() 中点(如图1).将
中点(如图1).将![]() 沿
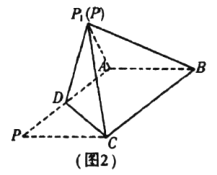
沿![]() 折起到图2中
折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.
(1)将![]() 沿
沿![]() 折起的过程中,
折起的过程中, ![]() 平面
平面![]() 是否成立?并证明你的结论;
是否成立?并证明你的结论;
(2)若![]() 与平面
与平面![]() 所成的角为60°,且
所成的角为60°,且![]() 为锐角三角形,求平面
为锐角三角形,求平面![]() 和平面
和平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)当DP1⊥DA时,CD⊥平面P1DA.由余弦定理得DC2=4,由勾股定理得DC⊥AD.即得到将△PCD沿CD折起的过程中,当DP1⊥DA时,CD⊥平面P1DA.(2)先证明![]() 在平面
在平面![]() 内的射影
内的射影![]() 必在棱
必在棱![]() 上,再建系,得到两个平面的法向量,得到两个法向量的夹角进而得到两个面的夹角。
上,再建系,得到两个平面的法向量,得到两个法向量的夹角进而得到两个面的夹角。
解析:
(1)将![]() 沿
沿![]() 折起过程中,
折起过程中, ![]() 平面
平面![]() 成立,
成立,
证明:∵![]() 是
是![]() 中点,∴
中点,∴![]() ,
,
在![]() 中,由余弦定理得,
中,由余弦定理得,
![]()
![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形且
为等腰直角三角形且![]() ,
,
∴![]() ,
, ![]() ,
, ![]()
∴![]() 平面
平面![]() .
.
(2)由(1)知![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
∵![]() 为锐角三角形,∴
为锐角三角形,∴![]() 在平面
在平面![]() 内的射影
内的射影![]() 必在棱
必在棱![]() 上(如图),
上(如图),
∴![]() 平面
平面![]() ,
,
则![]() 是
是![]() 和平面
和平面![]() 所成的角,
所成的角,
故![]() ,
,
∵![]() ,
,
∴![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 中点,
中点,
故以![]() 为坐标原点,过点
为坐标原点,过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴建立如图所示坐标系.
轴建立如图所示坐标系.

设![]() 轴于
轴于![]() 交于点
交于点![]() ,
,
∵![]() ,∴
,∴ ![]() ,
,
易知![]() ,
,
∴![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∵![]() 平面
平面![]() ,
,
∴可取平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 和平面
和平面![]() 所成的角为
所成的角为![]() ,
,
则 ,∴
,∴ 得
得
令![]() ,则
,则 ,
,
从而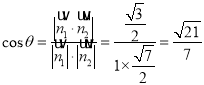 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某化工厂为预测产品的回收率![]() ,需要研究它和原料有效成分含量
,需要研究它和原料有效成分含量![]() 之间的相关关系,现收集了4组对照数据。
之间的相关关系,现收集了4组对照数据。
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(Ⅰ)请根据相关系数![]() 的大小判断回收率
的大小判断回收率![]() 与
与![]() 之间是否存在高度线性相关关系;
之间是否存在高度线性相关关系;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测当
,并预测当![]() 时回收率
时回收率![]() 的值.
的值.
参考数据: 
| 1 | 0 |
|
| 其他 |
| 完全相关 | 不相关 | 高度相关 | 低度相关 | 中度相关 |
 ,
, ![]()
