题目内容
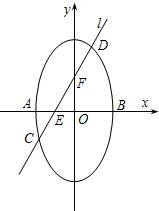 椭圆x2+
椭圆x2+| y2 |
| 4 |
(Ⅰ)若
| CE |
| FD |
(Ⅱ)设直线AD,CB的斜率分别为k1,k2,若k1:k2=2:1,求k的值.
分析:(Ⅰ)设C(x1,y1),D(x2,y2),由
得(4+k2)x2+2kx-3=0,再由判别式和根与系数的关系可推导出所求直线l的方程为2x-y+1=0或2x+y-1=0.
(Ⅱ)由题设知y12=4(1-x12),y22=4(1-x22),由此推出3x1x2+5(x1+x2)+3=0,所以3k2-10k+3=0,由此可推导出k的值.
|
(Ⅱ)由题设知y12=4(1-x12),y22=4(1-x22),由此推出3x1x2+5(x1+x2)+3=0,所以3k2-10k+3=0,由此可推导出k的值.
解答:解:(Ⅰ)设C(x1,y1),D(x2,y2),
由
得(4+k2)x2+2kx-3=0,
△=4k2+12(4+k2)=16k2+48,x1+x2=
,x1x2=
,(2分)
由已知E(-
,0),F(0,1),
又
=
,所以(-
-x1,-y1)=(x2,y2-1)(4分)
所以-
-x1=x2,即x2+x1=-
,(5分)
所以
=-
,解得k=±2,(6分)
符合题意,
所以,所求直线l的方程为2x-y+1=0或2x+y-1=0.(7分)
(Ⅱ)k1=
,k2=
,k1:k2=2:1,
所以
=
,(8分)
平方得
=4,(9分)
又
+
=1,所以y12=4(1-x12),同理y22=4(1-x22),代入上式,
计算得
=4,即3x1x2+5(x1+x2)+3=0,(12分)
所以3k2-10k+3=0,解得k=3或k=
,(13分)
因为
=
,x1,x2∈(-1,1),所以y1,y2异号,故舍去k=
,
所以k=3.(14分)
由
|
△=4k2+12(4+k2)=16k2+48,x1+x2=
| -2k |
| 4+k2 |
| -3 |
| 4+k2 |
由已知E(-
| 1 |
| k |
又
| CE |
| FD |
| 1 |
| k |
所以-
| 1 |
| k |
| 1 |
| k |
所以
| -2k |
| 4+k2 |
| 1 |
| k |
符合题意,
所以,所求直线l的方程为2x-y+1=0或2x+y-1=0.(7分)
(Ⅱ)k1=
| y2 |
| x2+1 |
| y1 |
| x1-1 |
所以
| y2(x1-1) |
| y1(x2+1) |
| 2 |
| 1 |
平方得
| ||
|
又
| x | 2 1 |
| ||
| 4 |
计算得
| (1-x2)(1-x1) |
| (1+x1)(1+x2) |
所以3k2-10k+3=0,解得k=3或k=
| 1 |
| 3 |
因为
| y2(x1-1) |
| y1(x2+1) |
| 2 |
| 1 |
| 1 |
| 3 |
所以k=3.(14分)
点评:本题考查圆锥曲线的综合运用,是历年高考题的重要题型之一,解题时要注意计算能力的培养,注意积累解题方法.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目