题目内容
利用计算机随机模拟方法计算y=x2与y=4所围成的区域Ω的面积时,可以先运行以下算法步骤:
第一步:利用计算机产生两个在[0,1]区间内的均匀随机数a,b;
第二步:对随机数a,b实施变换:
得到点A(a1,b1);
第三步:判断点A(a1,b1)的坐标是否满足b1<
;
第四步:累计所产生的点A的个数m,及满足b1<
的点A的个数n;
第五步:判断m是否小于M(一个设定的数).若是,则回到第一步,否则,输出n并终止算法.
若设定的M=100,且输出的n=34,则据此用随机模拟方法可以估计出区域Ω的面积为______(保留小数点后两位数字).
第一步:利用计算机产生两个在[0,1]区间内的均匀随机数a,b;
第二步:对随机数a,b实施变换:
|
第三步:判断点A(a1,b1)的坐标是否满足b1<
| a | 21 |
第四步:累计所产生的点A的个数m,及满足b1<
| a | 21 |
第五步:判断m是否小于M(一个设定的数).若是,则回到第一步,否则,输出n并终止算法.
若设定的M=100,且输出的n=34,则据此用随机模拟方法可以估计出区域Ω的面积为______(保留小数点后两位数字).
根据题意可得,点落在y=x2与y=4所围成的区域Ω的点的概率是
=
,
矩形的面积为4×4=16,阴影部分的面积为S,
则有
=
,
∴S=10.56.
故答案为:10.56.
| 100-34 |
| 100 |
| 66 |
| 100 |
矩形的面积为4×4=16,阴影部分的面积为S,
则有
| S |
| 16 |
| 66 |
| 100 |
∴S=10.56.
故答案为:10.56.

练习册系列答案
相关题目
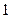 到
到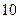 这
这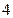 个,则任意两个数都不相邻的取法有多少种?
个,则任意两个数都不相邻的取法有多少种?