题目内容
18.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA.(I)求B的大小;
(Ⅱ)若b=2.求a+c的最值.
分析 (I)已知等式利用正弦定理化简,根据sinA不为0求出sinB的值,即可确定出B的大小;
(Ⅱ)由b与sinB的值,利用正弦定理求出2R的长,原式利用正弦定理化简,把表示出的C代入利用和差化积公式变形,利用余弦函数的值域即可确定出最值.
解答 解:(I)把a=2bsinA,利用正弦定理化简得:sinA=2sinAsinB,
∵sinA≠0,
∴sinB=$\frac{1}{2}$,
∵B为锐角,
∴B=30°;
(Ⅱ)∵B=30°,
∴A+C=150°,即C=150°-A,
由正弦定理得:$\frac{b}{sinB}$=2R,即2R=$\frac{2}{\frac{1}{2}}$=4,
∵sin75°=sin(45°+30°)=$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
∴a+c=2RsinA+2RsinC=4(sinA+sinC)=4[sinA+sin(150°-A)]=4×2sin75°cos(A-75°)=(2$\sqrt{6}$+2$\sqrt{2}$)cos(A-75°),
∵0<A<150°,即-75°<A-75°<75°,
∴0<cos(A-75°)≤1,
∵a+c>b=2,
∴a+c的最大值为2$\sqrt{6}$+2$\sqrt{2}$,最小值为2.
点评 此题考查了正弦定理,和差化积公式,余弦函数的定义域与值域,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.若集合A={x|x2+2ax+1=0}的子集只有一个,则a的集合( )
| A. | {-1,1} | B. | {a|-1<a<1} | C. | {a|-1≤a≤1} | D. | {a|<-1或a>1} |
17.(重点中学做)复数$\frac{1+{i}^{3}}{1+i}$=( )
| A. | i | B. | -i | C. | 1+i | D. | 1-i |
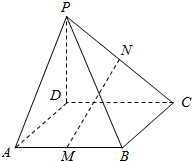 如图,在四棱锥P-ABCD中,M、N分别是AB、PC的中点.若ABCD是平行四边形.
如图,在四棱锥P-ABCD中,M、N分别是AB、PC的中点.若ABCD是平行四边形.