Question

【题目】已知椭圆 的离心率为，左、右焦点分别是,以为圆心、3为半径的圆与以为圆心、1为半径的圆相交，交点在椭圆C上．

（1）求椭圆C的方程；

（2）直线与椭圆C交于A,B两点，点M是椭圆C的右顶点直线AM与直线BM分别与y轴交于点PQ，试问以线段PQ为直径的圆是否过x轴上的定点？若是，求出定点坐标；若不是，说明理由．

Answer 1

【答案】（1）； （2）.

【解析】

（1）由题意可得，又离心率 ，可求，即可求出椭圆的标准方程（2）联立直线与椭圆方程，消元得一元二次方程，求出，写出点的坐标，

以线段PQ为直径的圆过x轴上的定点 ，则等价于恒成立，利用向量运算即可求出.

（1）由题意知，则．又，可得，

椭圆的方程为。

（2）以线段PQ为直径的圆过x轴上的定点．

由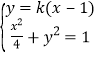 得．

设 ，则有

又点M是椭圆C的右顶点，所以点 ．

由题意可知直线AM的方程为，故点 ．

直线BM的方程为，故点．

若以线段PQ为直径的圆过x轴上的定点 ，则等价于恒成立．

又因为，

恒成立．

又因为 ，

所以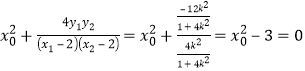 ．解得．

故以线段PQ为直径的圆过x轴上的定点。