题目内容
已知两点A、B分别在直线y=x和y=-x上运动,且|AB|= ,动点P满足
,动点P满足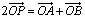 (O为坐标原点),点P的轨迹记为曲线C。
(O为坐标原点),点P的轨迹记为曲线C。
(1)求曲线C的方程;
(2)过曲线C上任意一点作它的切线l,与椭圆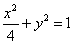 交于M、N两点,求证:
交于M、N两点,求证: 为定值。
为定值。
 ,动点P满足
,动点P满足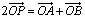 (O为坐标原点),点P的轨迹记为曲线C。
(O为坐标原点),点P的轨迹记为曲线C。(1)求曲线C的方程;
(2)过曲线C上任意一点作它的切线l,与椭圆
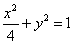 交于M、N两点,求证:
交于M、N两点,求证: 为定值。
为定值。解:(1)∵
∴P为线段AB的中点
∵A,B分别在直线y=x和y=-x上
∴
又
∴
∴点P在以原点为圆心, 为半径的圆上
为半径的圆上
∴点P的轨迹C的方程为 ;
;
(2)证明:当直线l的斜率存在时,设l:y=kx+m
∵l与C相切
∴
∴
联立
∴
设M(x1,y1),N(x2,y2),则 ,
,
又
∴ ·
· =0
=0
当直线l的斜率不存在时,l的方程为
带入椭圆方程得 或
或

此时,
综上所述 为定值0。
为定值0。

∴P为线段AB的中点
∵A,B分别在直线y=x和y=-x上
∴

又

∴

∴点P在以原点为圆心,
 为半径的圆上
为半径的圆上∴点P的轨迹C的方程为
 ;
;(2)证明:当直线l的斜率存在时,设l:y=kx+m
∵l与C相切
∴

∴

联立

∴

设M(x1,y1),N(x2,y2),则
 ,
,
又

∴
 ·
· =0
=0当直线l的斜率不存在时,l的方程为

带入椭圆方程得
 或
或

此时,

综上所述
 为定值0。
为定值0。
练习册系列答案
相关题目
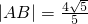 ,动点P满足
,动点P满足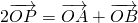 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C. 交于M、N两点,求证:
交于M、N两点,求证: 为定值.
为定值. ,动点P满足
,动点P满足 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C. 交于M、N两点,求证:
交于M、N两点,求证: 为定值.
为定值. ,动点P满足
,动点P满足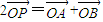 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C. 交于M、N两点,求证:
交于M、N两点,求证: 为定值.
为定值.