题目内容
已知两点A、B分别在直线y=x和y=-x上运动,且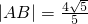 ,动点P满足
,动点P满足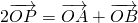 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C.
(1)求曲线C的方程;
(2)过曲线C上任意一点作它的切线l,与椭圆 交于M、N两点,求证:
交于M、N两点,求证: 为定值.
为定值.
解:(1)(方法一)设P(x,y),A(x1,x1),B(x2,-x2).
∵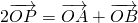 ,∴P是线段AB的中点,∴
,∴P是线段AB的中点,∴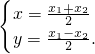 (2分)
(2分)
∵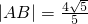 ,∴
,∴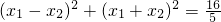 ,∴
,∴ .
.
∴化简得点P的轨迹C的方程为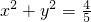 .(5分)
.(5分)
(方法二)∵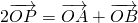 ,∴P为线段AB的中点、(2分)
,∴P为线段AB的中点、(2分)
∵M、N分别在直线y=x和y=-x上,∴∠AOB=90°.
又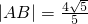 ,∴
,∴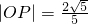 ,∴点P在以原点为圆心,
,∴点P在以原点为圆心, 为半径的圆上、
为半径的圆上、
∴点P的轨迹C的方程为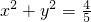 .(5分)
.(5分)
(2)证明:当直线l的斜率存在时,设l:y=kx+m,
∵l与C相切,∴ =
= ,∴
,∴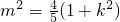 .
.
联立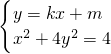 ,∴
,∴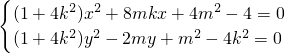 .
.
设M(x1,y1),N(x2,y2),则x1•x2=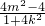 ,
,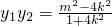 .(8分)
.(8分)
∴ •
• =x1x2+y1y2=
=x1x2+y1y2= .
.
又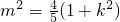 ,∴
,∴ •
• =0.(10分)
=0.(10分)
当直线l的斜率不存在时,l的方程为x=± ,代入椭圆方程得
,代入椭圆方程得
M( ,
, ),N(
),N( ,-
,- )或M(-
)或M(- ,
, ),N(-
),N(- ,-
,- ),
),
此时, •
• =
= -
- =0.
=0.
综上所述, •
• 为定值0.(12分)
为定值0.(12分)
分析:(1)(方法一)设P(x,y),A(x1,x1),B(x2,-x2).由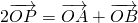 ,知P是线段AB的中点,由此能得到点P的轨迹C的方程.
,知P是线段AB的中点,由此能得到点P的轨迹C的方程.
(方法二)由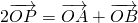 ,知P为线段AB的中点,由M、N分别在直线y=x和y=-x上,知∠AOB=90°.由此能得到点P的轨迹C的方程.
,知P为线段AB的中点,由M、N分别在直线y=x和y=-x上,知∠AOB=90°.由此能得到点P的轨迹C的方程.
(2)当直线l的斜率存在时,设l:y=kx+m,由l与C相切,知 =
= ,
,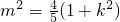 .联立
.联立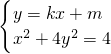 ,故
,故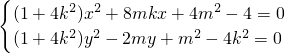 .由此能够证明
.由此能够证明 •
• 为定值0.
为定值0.
点评:本小题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆、椭圆的相关知识.
∵
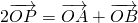 ,∴P是线段AB的中点,∴
,∴P是线段AB的中点,∴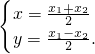 (2分)
(2分)∵
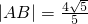 ,∴
,∴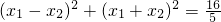 ,∴
,∴ .
.∴化简得点P的轨迹C的方程为
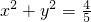 .(5分)
.(5分)(方法二)∵
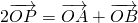 ,∴P为线段AB的中点、(2分)
,∴P为线段AB的中点、(2分)∵M、N分别在直线y=x和y=-x上,∴∠AOB=90°.
又
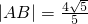 ,∴
,∴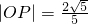 ,∴点P在以原点为圆心,
,∴点P在以原点为圆心, 为半径的圆上、
为半径的圆上、∴点P的轨迹C的方程为
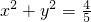 .(5分)
.(5分)(2)证明:当直线l的斜率存在时,设l:y=kx+m,
∵l与C相切,∴
 =
= ,∴
,∴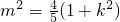 .
.联立
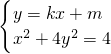 ,∴
,∴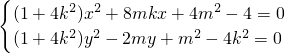 .
.设M(x1,y1),N(x2,y2),则x1•x2=
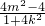 ,
,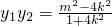 .(8分)
.(8分)∴
 •
• =x1x2+y1y2=
=x1x2+y1y2= .
.又
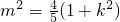 ,∴
,∴ •
• =0.(10分)
=0.(10分)当直线l的斜率不存在时,l的方程为x=±
 ,代入椭圆方程得
,代入椭圆方程得M(
 ,
, ),N(
),N( ,-
,- )或M(-
)或M(- ,
, ),N(-
),N(- ,-
,- ),
),此时,
 •
• =
= -
- =0.
=0.综上所述,
 •
• 为定值0.(12分)
为定值0.(12分)分析:(1)(方法一)设P(x,y),A(x1,x1),B(x2,-x2).由
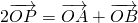 ,知P是线段AB的中点,由此能得到点P的轨迹C的方程.
,知P是线段AB的中点,由此能得到点P的轨迹C的方程.(方法二)由
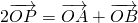 ,知P为线段AB的中点,由M、N分别在直线y=x和y=-x上,知∠AOB=90°.由此能得到点P的轨迹C的方程.
,知P为线段AB的中点,由M、N分别在直线y=x和y=-x上,知∠AOB=90°.由此能得到点P的轨迹C的方程.(2)当直线l的斜率存在时,设l:y=kx+m,由l与C相切,知
 =
= ,
,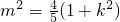 .联立
.联立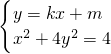 ,故
,故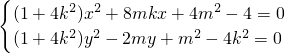 .由此能够证明
.由此能够证明 •
• 为定值0.
为定值0.点评:本小题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆、椭圆的相关知识.

练习册系列答案
相关题目
 ,动点P满足
,动点P满足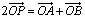 (O为坐标原点),点P的轨迹记为曲线C。
(O为坐标原点),点P的轨迹记为曲线C。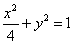 交于M、N两点,求证:
交于M、N两点,求证: 为定值。
为定值。 ,动点P满足
,动点P满足 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C. 交于M、N两点,求证:
交于M、N两点,求证: 为定值.
为定值. ,动点P满足
,动点P满足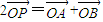 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C. 交于M、N两点,求证:
交于M、N两点,求证: 为定值.
为定值.