题目内容
7.用“五点法”作出函数y=1-2sinx,x∈[-π,π]的简图,并回答下列问题:(1)观察函数图象.写出满足下列条件的x的区间,①y>1;②y<1.
(2)若直线y=a与y=1-2sinx,x∈[-π,π]有两个交点,求a的取值范围.
分析 (1)用五点作图法画出函数图象,观察图象,即可写出满足条件的x的区间;
(2)根据图象,用数形结合,判断交点个数.即可求出a的取值范围.
解答 解:用“五点法”作出函数y=1-2sinx,x∈[-π,π]的简图:列表为
| x | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | π |
| 2sinx | 0 | -2 | 0 | 2 | 0 |
| y=1-sinx | 1 | 3 | 1 | -1 | 1 |
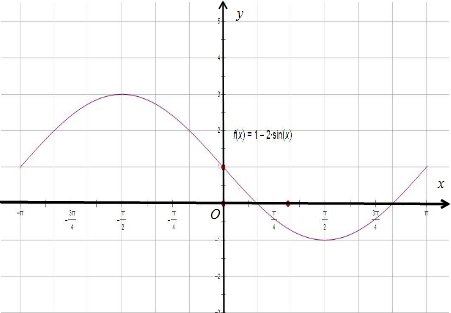
(1)观察函数图象.满足①y>1的x的区间是:(-π,0)
满足②y<1的x的区间是:(0,π),
(2)若直线y=a与y=1-2sinx,x∈[-π,π]有两个交点,由图象可知:
当1<a<3时,直线y=a与y=1-2sinx,x∈[-π,π]有两个交点,
当-1<a<1时,直线y=a与y=1-2sinx,x∈[-π,π]有两个交点,
故a的取值范围是:(-1,1)∪(1,3).
点评 本题考查了正弦函数的图象,考查了五点作图法,数形结合思想是高中重要的一种思想,应熟练灵活掌握,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),下面四个图象中,y=f(x)的图象大致是( )
已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),下面四个图象中,y=f(x)的图象大致是( )



 给出一个如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的集合为{0,1,3}.
给出一个如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的集合为{0,1,3}.