题目内容
【题目】如图：点P在直径AB=1的半圆上移动（点P不与A，B重合），过P作圆的切线PT且PT=1，∠PAB=α，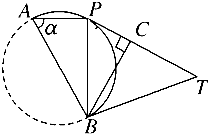
（1）当α为何值时，四边形ABTP面积最大？
（2）求|PA|+|PB|+|PC|的取值范围？
【答案】
（1）解：∵AB为直径，
∴∠APB=90°，AB=1，
∵∠PAB=α，
∴PA=cosα，PB=sinα，
又PT切圆于P点，∠TPB=∠PAB=α，
∴BC=sinαPB=sin2α，
∴S四边形ABTP=S△PAB+S△TPB
= 
PAPB+ PTBC
= sinαcosα+ sin2α
= 
sin2α+ （1﹣cos2α）
= （sin2α﹣cos2α）+
= 
sin（2α﹣ 
）+ ，
∵0＜α＜ 
，﹣ ＜2α﹣ ＜ 
π，
∴当2α﹣ = ，即α= 
π时，S四边形ABTP最大
（2）解：|PA|+|PB|+|PC|=cosα+sinα+sinαcosα，
设t=cosα+sinα，则t2=cos2α+sin2α+2cosαsinα=1+2cosαsinα，
∴cosαsinα= 
，
∴|PA|+|PB|+|PC|= +t= 
+t﹣ ，
∵t=cosα+sinα= 
sin（α+ ）∈1， ]，且t=﹣1（1， ]，
∴|PA|+|PB|+|PC|= +t﹣ 在t∈（1， ]时单调递增，
则（|PA|+|PB|+|PC|）∈（1， + ]
【解析】（1）由AB为圆的直径，利用圆周角定理得到∠APB为直角，再由AB=1，表示出PA与PB，根据PT与圆相切，表示出BC，进而表示出四边形ABTP的面积，整理后，利用正弦函数的值域及二次函数性质确定出最大值即可；（2）把表示出的PA，PB，PC代入所求式子，设t=cosα+sinα，可得出t2=1+2cosαsinα，进而表示出cosαsinα，代入所求式子整理为一个角的正弦函数，利用正弦函数的值域及二次函数性质确定出范围即可．
